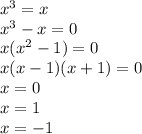
Подкоренное выражение 7х - х² должно быть положительным или равным нулю, потому что извлекать квадратный корень из отрицательного числа нельзя.
7х - х² ≥ 0.
Решим неравенство методом интервалов. Найдем нули функции.
7х - х² = 0.
Вынесем за скобку общий множитель х.
х(7 - х) = 0.
Произведение двух множителей равно нулю тогда, когда один из множителей равен нулю.
1) х = 0;
2) 7 - х = 0;
х = 7.
Отметим на числовой прямой точки 0 и 7.
Эти числа делят числовую прямую на интервалы 1) (-∞; 0], 2) [0; 7], 3) [7; +∞).
Выясним, на каком из интервалов выражение 7х - х² будет принимать положительные значения. На 1 и 3 интервалах это выражение отрицательно, на 2 итервале - положительно. Поэтому, значения х, принадлежащие 2 интервалу являются областью определения функции.
ответ. [0; 7].
ОДЗ :
x² - 2x - 8 > 0
(x - 4)(x + 2) > 0
+ - +
_____________₀__________₀___________
- 2 4
////////////////////////// ///////////////////////////
x ∈ ( - ∞ , - 2) ∪ (4 ; + ∞)
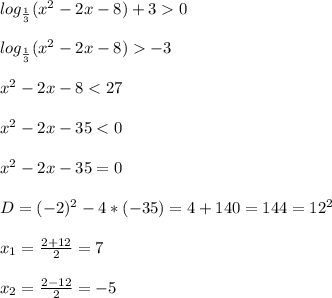
+ - +
______________₀_____________₀_____________
- 5 7
////////////////////////////
x ∈ (- 5 , 7)
С учётом ОДЗ окончательный ответ :
x ∈ (- 5 ; - 2) ∪ (4 , 7)
x(x²-1)=0
x(x-1)(x+1)=0
x=0
x=1
x=-1