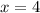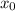к положительному направлению оси х равен значению производной этой функции в точке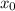 
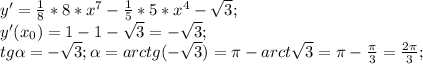Или 120 градусов
Вероятность выигрыша 0,5, значит вероятность проигрыша 1-0,5=0,5
Найти количество билетов чтобы вероятность выигрыша была
не менее 0,999
Решим альтернативную задачу: найдем количество билетов, чтобы вероятность проигрыша была менее 0,001
первый билет проиграл 0,5
значит берем второй билет и он тоже проиграл 0,5*0,5=0,25>0.001
значит берем третий билет и он тоже проиграл 0,25*0,5=0,125>0.001
четвертый 0,125*0,5=0,0625>0,001
пятый 0,0625*0,5=0,03125>0.001
шестой 0,03125*0,5=0,015625>0,001
седьмой 0,015625*0,5=0,0078125>0.001
восьмой 0.0078125*0.5=0.00390625>0,001
девятый 0,0039*0,5=0,00195>0.001
десятый 0.00195*0.5=0.00097 <0.001
Значит среди 10 билетов хотя бы один будет выигрышный
Рассмотрим функцию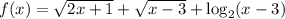 
на её области определения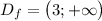 
График этой функции пересечёт линию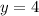 
более одного раза только если будут существовать промежутки разной монотонности (на каких-то функция возрастает, на других - убывает).
Обязательным условием смены монотонности функции является обращение её производной в ноль (или несуществование производной) в точке, где монотонность меняется. Попробуем их найти.
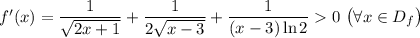
Как видно из вида производной, для всех точек области определения функции, она не обращается в ноль (более того, функция строго возрастает).
Таким образом, наше уравнение не может иметь более одного корня.
Методом пристального взгляда замечаем, что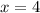 
- корень уравнения.
Действительно,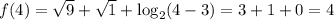 
ответ.
