Объяснение:
1.
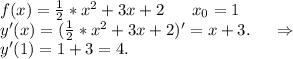
ответ: y'(1)=4.
2.

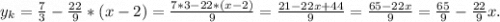
3.
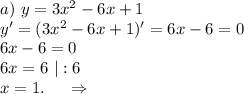
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(-∞;1) функция убывает.
При х∈(1;+∞) фунуция возрастает .
![b)\ y=x^9-9x\\y'=(x^9-9x)'=9x^8-9=9*(x^8-1)=0\\9*(x^8-1)=0\ |:9\\x^8-1=0\\x^8=1\\x=\sqrt[8]{1}\\x_1=-1\ \ \ \ x_2=1](/tpl/images/1848/3010/401ca.png)
В окрестности точки x = -1 производная функции меняет знак с (+) на (-). Следовательно, точка x = -1 - точка максимума.
При х∈(-∞;-1) фунуция возрастает .
В окрестности точки x = 1 производная функции меняет знак с (-) на (+). Следовательно, точка x = 1 - точка минимума.
При х∈(1;+∞) функция возрастает. ⇒
При х∈(-1;1) функция убывает.
1. Воспользуемся формулой разности квадратов:
2. Приводим подобные:
3. Сокращаем дробь: