x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
Объяснение:
находим ОДЗ x ∉ [ -1, -1/3 ] отсюда>>
область допустимых значений: x ∈ (-∞,-1) ∪ (-1/3, +∞)
Для а>1 выражение log a(x) ≥ log a(y) равно x≥y
4x^2 + 1 ≥ 3x^2 + 4x + 1
4x^2 ≥ 3x^2 + 4x
4x^2 - 3x^2 - 4x ≥ 0
x^2 - 4x ≥ 0
x ( x - 4 ) ≥ 0
возможны 2 случая когда произведение a*b будет ≥ 0.
(либо два отрицательных)
(либо два положительных)
Проверяем
x≥0 <=> x≥0 <=> x ∈ [4 , +∞ )
x-4≥0 x≥4
x ≤ 0 <=> x≤0 <=> x ∈ ( - ∞, 0 ]
x - 4 ≤0 x≤4
находим объединение для x ∈ ( - ∞, 0 ] и x ∈ [4 , +∞ ), получаем множество решений
МНОЖЕСТВО РЕШЕНИЙ x∈ (- ∞,0] ∪ [4, +∞) ,
ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ x ∈ (-∞,-1) ∪ (-1/3, +∞)
нахождение пересечения множеств решений и области допустимых значений
x ∈ (-∞, -1) ∪ (-1/3, 0] ∪ [4, +∞)
(см. объяснение)
Объяснение:
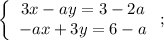
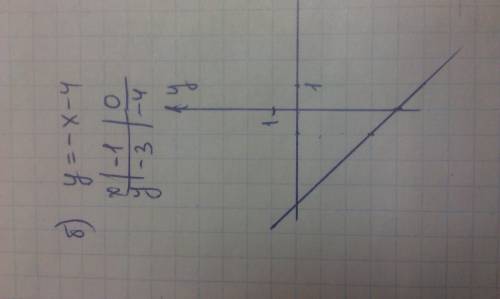
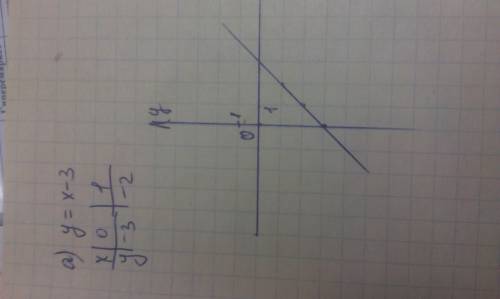
Перед нами система из уравнений, графиком каждого из которых является прямая. Применим геометрию и вспомним, что прямые могут пересекаться, совпадать или быть параллельными. В каждом из случаев будет одно решение, их бесконечное множество, отсутствие решений соответсвенно. Нас устраивает первый случай. Опишем его на языке математики, как 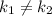 , где
, где 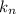 - это угловой коэффициент (тангенс угла наклона).
- это угловой коэффициент (тангенс угла наклона).
Тогда выразим 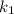 и
и 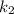 из строк исходной системы.
из строк исходной системы.
При 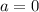 :
:
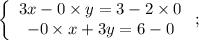
Решением будет пара чисел 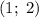 .
.
Значит такое значение параметра нам подходит.
При 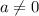 :
:
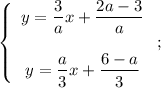
Тогда:
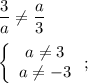
Итого получили, что при 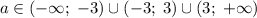 исходная система уравнений имеет ровно одно решение.
исходная система уравнений имеет ровно одно решение.
Задание выполнено!
Б) 1-2-4=0
Вот все вроде бы