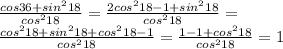
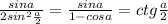
Объяснение:
Русская рулетка подчиняется общим законам теории вероятности.
Если считать револьвер шестизарядным с одним патроном в барабане и если барабан не вращается рукой после каждого спуска курка, то вероятность выстрела P с каждой новой попыткой будет увеличиваться пропорционально уменьшению оставшегося количества.
P=1/(N-n),
где P — вероятность выстрела, N — количество гнезд в барабане, n — количество сделанных ходов.
Таким образом, если пять раз револьвер не выстрелил, то известно, что он выстрелит при шестой попытке.
В нашем же случае, в барабане имеется 5 гнёзд. Следовательно:
Р₁=1/(5-0)=1/5 => Вероятность выжить=1-1/5=4/5=80%
Р₂=1/(5-1)=1/4 => Вероятность выжить=3/4=75%
Р₃=1/(5-3)=1/3; Вероятность выжить=2/3=66.6%
Р₄=1/2; Вероятность выжить=1/2=50%
Р₅=1; Вероятность выжить=0%
Таким образом, вероятность того, что револьвер не выстрелит 4 раза подряд будет равна: Р=4/5*3/4*2/3*1/2= 1/5= 20%
a x^{2} +bx + c = a(x - x_{1} )(x - x_{2} )
Где, x_{1} и x_{2} - корни уравнения
a) x^{2} +14x + 48 = 0
D = 14^{2} - 4*1*48 = 4 = 2^{2}
x_{1} = \frac{-14+2}{2} = -6
x_{2} = \frac{-14-2}{2} = 8
x^{2} +14x + 48 = (x - (-6))(x - (-8)) = (x+6)(x+8)
b) 25 x^{2} -10x-12 =0
D = (-10)^{2} - 4*25*(-12) = 1300= (10 \sqrt{13}) ^{2}
x_{1} = \frac{-(-10 +10 \sqrt{13})}{2*25} = \frac{1}{5} + \frac{1}{5} \sqrt{13}
x_{2} = \frac{-(-10 -10 \sqrt{13})}{2*25} = \frac{1}{5} - \frac{1}{5} \sqrt{13}
Подставляем в формулу:
25 x^{2} -10x-12 = 25(x - ( \frac{1}{5} + \frac{1}{5} \sqrt{13} ))(x - (\frac{1}{5} - \frac{1}{5} \sqrt{13}) ) = (25x -5 + 5 \sqrt{13} )(x - (\frac{1}{5} - \frac{1}{5} \sqrt{13}) ) = (25x -5 + 5 \sqrt{13} )(x -\frac{1}{5} + \frac{1}{5} \sqrt{13}))