x ∈ [⅔; 6)
Объяснение:
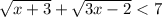
ОДЗ:
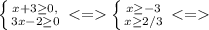 x ∈ [⅔; +∞)
x ∈ [⅔; +∞)
Возводим в квадрат обе части уравнения:
(√(x + 3) + √(3x - 2))² < 7²
Решаем:
x + 3 + 2√((x + 3)(3x-2)) + 3x - 2 < 49
4x + 1 + 2√(3x² + 7x - 6) < 49
2√(3x² + 7x - 6) < 48 - 4х | :2
√(3x² + 7x - 6) < 24 - 2x
Имеем два случая:
Если 1) 24 - 2x < 0, то нет корней;
2) 24 - 2x ≥ 0
(√(3x² + 7x - 6))² < (24 - 2x)² при 24 - 2x ≥ 0
ОДЗ: 3x² + 7x - 6 ≥ 0; (x+3)*(3x - 2) ≥ 0
+ - +
------•------•------>
-3 ⅔
ОДЗ: x ∈ (-∞; -3] ∪ [⅔; +∞)
Решаем далее:
3x² + 7x - 6 < 4x² - 96x + 576
-x² + 103x - 582 < 0
(x - 6)*(x - 97) > 0 *корни уравнения x² - 103x + 582 = 0 были найдены по т-ме Виета
+ - +
------о------о------>
6 97
х ∈ (-∞; 6) ∪ (97; +∞)
Так как мы взяли 24 - 2х ≥ 0, то: 24 ≥ 2x; x ≤ 12.
х ∈ (-∞; 6) ∪ (97; +∞) при x ≤ 12, то у нас решение первого нер-ва: х ∈ (-∞; 6).
В итоге, решением заданного по условию неравенства является решение 1-го полученного неравенства и ограничения начального неравенства:
х ∈ (-∞; 6) при x ∈ [⅔; +∞)
Пересечением данных неравенств является интервал: x ∈ [⅔; 6). Это и будет ответом.
ответ: (√х-6)²-1=0 равносильно уравнению 2x-6√x=6√x+x-35.
Объяснение:
Два уравнения будут равносильными, если они имеют одно и то же множество корней (в случае кратных корней кратности соответствующих корней должны совпадать.)
Решим данное уравнение.
2x-6√x=6√x+x-35; x-12√x+35=0, по Виета √х=5⇒х=25; √х=7⇒х=49, т.е. данное уравнение имеет два корня 25 и 49.
Проверим сначала, являются ли эти корни корнями оставшихся уравнений. 1) (√25+5)²-1=0, т.к. 99≠0, то второй корень можно и не проверять.
2) √(25+6)²-1=0; т.к. 120≠0, второй корень тоже не проверяем.
3) т.к. при переносе вправо единицы получим (√х+6)²=-1, чего быть не может, то это уравнение вообще не имеет корней.
Т.е. первые три уравнения не равносильны данному. Проверим четвертое.
4) (√25-6)²-1=0; 0=0; ( √49-6)²-1=0; 0=0- верное равенство. Значит, корни четвертого уравнения являются корнями первого. Других корней у последнего уравнения нет , т.к. (√x-6)²-1=0 можно упростить , получим
х-12√x+36-1=0;х-12√x+35=0- а это и есть первое уравнение.
Вывод четвертое уравнение равносильно уравнению, данному в условии задачи.
х -1; -0,5; 0; 1; 0,5; 2
у 7; 2; -1; -1; -2; 7