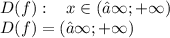и 
. Чтобы найти координату 
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
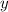можем найти подставив в выражение первой функции , а можно сделать проще. Так как пересечение будет с прямой , то и точки пересечения будут иметь координату . Итак, получилось две точки пересечения с координатами: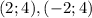 
.![[0;1]](/tpl/images/0561/5883/90495.png)
(этот отрезок по оси ), найдем значения на концах этого отрезка: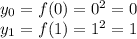
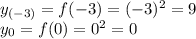
Общий вид функции
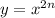
Верное свойство данной функции 3):
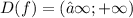
Объяснение:
Я так понимаю, имелось в виду следующее:
Дана функция
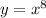
Общий вид данной функции:
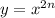
Потому что показатель степени у данной функции равен 8, т е. четный:
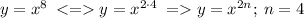
Выбери верное свойство данной функции:
1.D(f)=(−∞;0] - Неверно.
Данная функция определена как для положительных, так и для отрицательных значений аргумента
![1. \quad \: \cancel{D(f)=(−∞;0] } \\](/tpl/images/1610/0071/c3970.png)
2. Ф-ия нечётная - НЕверно
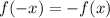
Проверим функцию на нечетность. Нечетной называется функция, если f(-x) = -f(x)
В нашем случае
3. D(f)=(−∞;+∞) - ВЕРНО!
ДАННАЯ ФУНКЦИЯ ОПРЕДЕЛЕНА ДЛЯ ЛЮБЫХ ДЕЙСТВИТЕЛЬНЫХ ЗНАЧЕНИЙ Х:
