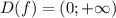- интервал (0; 3) принадлежит этому множеству, и функция там непрерывна.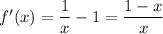
Случайная величина Х - число попаданий в мишень - может принимать значения 0,1,2,3,4. Найдём соответствующие вероятности:
p0=0,5*0,5*0,6*0,6=0,09
p1=0,5*0,5*0,6*0,6+0,5*0,5*0,6*0,6+0,5*0,5*0,4*0,6+0,5*0,5*0,6*0,4=0,3
p2=0,5*0,5*0,6*0,6+0,5*0,5*0,4*0,6+0,5*0,5*0,6*0,4+0,5*0,5*0,4*0,6+0,5*0,5*0,6*0,4+0,5*0,5*0,4*0,4=0,37
p3=0,5*0,5*0,4*0,6+0,5*0,5*0,4*0,4+0,5*0,5*0,4*0,4+0,5*0,5*0,6*0,4=0,2
p4=0,5*0,5*0,4*0,4=0,04.
Проверка: p0+p1+p2+p3+p4=1, так что все вероятности найдены верно.
Составляем закон распределения случайной величины X:
X 0 1 2 3 4
P 0,09 0,3 0,37 0,2 0,04
(cosx*cos(2x)/sin(2x)) - (sinx*sin(2x)/sin(2x)) = -sinx
cosx*(2cos^2(x) - 1)/(2sinx*cosx) - sinx = -sinx
(2cos^2(x) - 1)/(2sinx) = 0
2cos^2(x) - 1 = 0
cos^2(x) = 1/2
1) cosx = √2/2
x = +-π/4 + 2πk
2) cosx = -√2/2
x = +-3π/4 + 2πk
Объединяем решения 1) и 2), получаем:
x = π/4 + πk/2