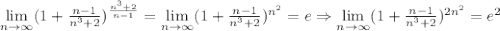В решении.
Объяснение:
Из пункта А в пункт В, расстояние между которыми 210 км, одновременно выехали два автомобиля. Так как скорость первого автомобиля на 5 км/ч больше скорости второго, то первый автомобиль в пункт назначения прибыл на 12 мин раньше, чем второй. Найдите скорость каждого из автомобилей.
Формула движения: S=v*t
S - расстояние v - скорость t – время
Таблица:
v (км/час) S (км) t (час)
1 автомобиль х 210 210/х
2 автомобиль х - 5 210 210/(х - 5)
По условию задачи разница во времени 12 минут = 0,2 часа, уравнение:
210/(х - 5) - 210/х = 0,2
Умножить все части уравнения на х(х - 5), чтобы избавиться от дробного выражения:
210х - 210х + 1050 = 0,2х² - х
-0,2х² + х + 1050 = 0
Разделить все части уравнения на -0,2 для упрощения:
х² - 5х - 5250 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 25 + 21000 = 21025 √D=145
х₁=(-b-√D)/2a
х₁=(5-145)/2 = -140/2 = -70, отбросить, как отрицательный;
х₂=(-b+√D)/2a
х₂=(5+145)/2
х₂=150/2
х₂=75 (км/час) - скорость первого автомобиля;
75 - 5 = 70 (км/час) - скорость второго автомобиля;
Проверка:
210 : 75 = 2,8 (часа);
210 : 70 = 3 (часа);
3 - 2,8 = 0,2 (часа) - верно.
Мастера получат 16 порций мороженого
Объяснение:
Задание:
Мастера Винтик и Шпунтик организовали Небольшую Артель Технического Обслуживание (НАТО). При выполнении одного задания Винтик получает определенное количество порций мороженого, а Шпунтик другое, но тоже фиксированное количество порций. За первый день работы Винтик выполнил 20 заказов, а Шпунтик 12, при этом вместе они съели 84 порции мороженого; за второй день Винтик выполнил 16 заказов, а Шпунтик 10, при этом вместе они съели 68 порций мороженого. Сколько порций мороженого съедят обессиленные партнеры по «агрессивному блоку», если Винтиқ выполнит 4 заказа, а Шпунтик 2 заказа?
Пусть х - количество порций мороженого, которое получает Винтик за выполнении 1-го заказа, а у - количество порций мороженого, которое получает Шпунтик за выполнении 1-го заказа.
Тогда за 1-й день они получили 20х + 12у порций, количество которых по условию равно 84.
20х + 12у = 84 или 5х + 3у = 21 (1)
За 2-й день они получили 16х + 10у порций, что по условию составляет 68 порций
16х + 10у = 68 или 8х + 5у + 34 (2)
Решаем систему уравнений
5х + 3у = 21 | ·(-5) -25x - 15y = -105 складываем
8х + 5у = 34 | ·3 24x + 15y = 102 уравнения
-х = -3
х = 3 порции получает Винтик за 1 заказ
Из уравнения (1)
3у = 21 - 5х = 21 - 5 · 3 = 6
у = 2 порции получает Шпунтик за 1 заказ
За 4 заказа Винтик получит 3 · 4 = 12 (порций)
За 2 заказа Шпунтик получит 2 · 2 = 4 (порции)
Всего они получат
12 + 4 = 16 порций мороженого
Преобразуем: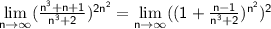
Из второго замечательного предела следует: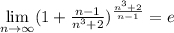 ;
;
Однако