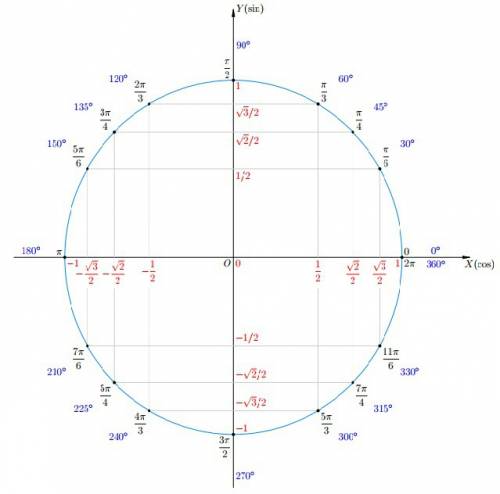
![[ -\frac{\pi}{2} ; \frac{\pi}{2} ]](/tpl/images/0597/4634/fea20.png) возрастает, а на промежутке
возрастает, а на промежутке ![[ \frac{\pi}{2} ; \frac{3\pi}{2} ]](/tpl/images/0597/4634/d8073.png) - убывает
- убывает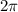 , то:
, то:![[ -\frac{\pi}{2}+2\pi n ; \frac{\pi}{2}+2\pi n ],n\in Z](/tpl/images/0597/4634/22506.png) - промежутки возрастания синусоиды
- промежутки возрастания синусоиды![[ \frac{\pi}{2}+2\pi n ; \frac{3\pi}{2}+2\pi n ],n\in Z](/tpl/images/0597/4634/745d6.png) - промежутки убывания синусоиды
- промежутки убывания синусоиды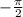 и точка
и точка 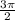 - одна и та же точка на тригонометрическом круге
- одна и та же точка на тригонометрическом круге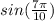 и
и 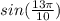
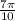
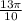
![[ \frac{\pi}{2} ; \frac{3\pi}{2} ]](/tpl/images/0597/4634/d8073.png) убывания. Так как это промежуток убывания, то если выполняется
убывания. Так как это промежуток убывания, то если выполняется 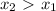 , то будет выполнятся
, то будет выполнятся 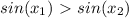
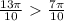
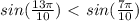
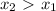 , то выполняется
, то выполняется 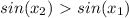
![[ \frac{3\pi}{2} ; \frac{5\pi}{2}]](/tpl/images/0597/4634/0c4f5.png)
![[- \frac{3\pi}{2} ; -\frac{\pi}{2} ]](/tpl/images/0597/4634/7af0d.png)
![[ \frac{3\pi}{2} ; \frac{5\pi}{2} ]](/tpl/images/0597/4634/5d6a9.png)
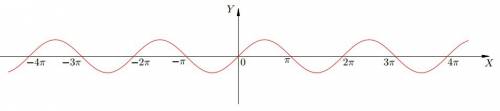
значит имеем такие решения