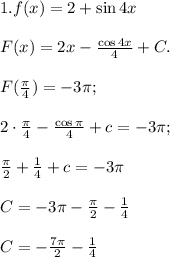
Заданная первообразная - 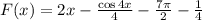
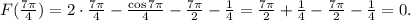
ОТВЕТ: 0.
![2. f(x)=e^x+2x+1, \max_{[0;2]}F(x)=e^2.\\\\F(x)=e^x+x^2+x+C.](/tpl/images/1075/3849/89ce2.png)
График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.
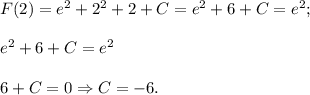
Заданная первообразная - 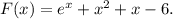
Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.
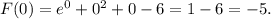
ОТВЕТ: -5.
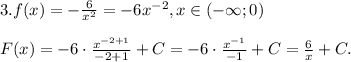
По условию 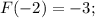
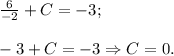
Заданная первообразная - 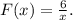
Решим уравнение 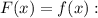
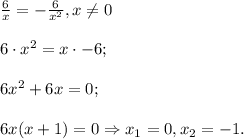
Однако вспоминаем про ограничение для самой переменной: 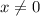 (о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение
(о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение 
ОТВЕТ: {-1}.
Область определения функции будет [2;+бесконечности) потому что у нас под корнем должно стоять не отрицательное число.
Решаем уравнение. Т.к. в правой части никогда не будет отрицательного числа(область определения не позволит) мы может возвести обе части уравнения в квадрат и получим
25(х-2)=х²+4х+4
Оно сводится к обычному квадратному
Х²+4х+4-25х+50=0
Х²-21х+54=0
По т. Виетта проиведение равняется колфиценту С, а сумма с противоположным знаком колфиценту В
Х1+Х2=21
Х1*Х2=54
Подходят числа 3 и 18, которые оба входят в область определения, значит оба являются ответом (можете решить через дискриминант, если вам удобно, тоже самое получите)
ответ:1)область определения [2;+бесконечности)
2) Х1=3 Х2=18
раз нужно чётное число, то последняя (третья) цифра- это 0, 2, или 4
то есть для третьей цифры есть эти три варианта
раз нужно трёхзначное, то первая цифра не может быть равна нулю
значит, ноль может быть использован только в третьей или второй цифре
1) если третья цифра- ноль, то для второй остаётся четыре варианта: 1, 2, 3, 4,
а для первой- три варианта (исключая цифру, поставленную второй)
2) если третья цифра- 2, то для второй остаётся четыре варианта: 0, 1, 3, 4
а для первой- три варианта (если вторая цифра- это ноль)
и два варианта (если вторая цифра не ноль, а 1, 3 или 4)
3) если третья цифра- 4, то получится то же, что и в варианте 2)
считаем количество комбинаций:
для 1) это: 1 * 4 * 3 = 12 разных чисел
а для двух вариантов 2) и 3) вместе это: 1*(1*3 + 3*2) * 2 варианта = 18 разных чисел
Итого, можно составить: 12 + 18 = 30 разных трёхзначных чисел
Можно начать считать варианты наоборот, начиная с первой цифры трёхзначного числа:
итак нам даны 3 чётных и 2 нечётных цифры: 0, 2, 4 и 1, 3
из них, для первой цифры можно использовать 2 чётных и 2 нечётных (т.к. ноль исключаем), а для третьей цифры можно использовать только чётные.
1) если ставим 1ую цифру чётную, то для 2ой цифры остаются 2 чётных и 2 нечётных
1а) если ставим 2ую цифру чётную, то для 3ей остаётся только 1 чётная цифра
1б) если ставим 2ую цифру нечётную, то для 3ей остаются 2 чётных варианта цифр
2) если ставим 1ую цифру нечётную, то для 2ой цифры остаются 3 чётных и 1 нечётная
2а) если ставим 2ую цифру чётную, то для 3ей остаются 2 чётных варианта цифр
2б) если ставим 2ую цифру нечётную, то для 3ей остаются 3 чётных варианта цифр
Считаем варианты, начиная с первой цифры: 2 чётных варианта первой цифры, каждый даёт по 2 чётных и 2 нечётных варианта второй цифры, из которых первые два- каждый даёт по 1 варианту 3ей цифры, а вторые два- каждый даёт по 2 варианта для 3ей цифры.
То есть получаем: 2 * ( 2*2 + 2*1 ) = 12 вариантов, если первая цифра- чётная.
Так же считаем для нечётной первой цифры: 2 нечётных варианта первой цифры, каждый даёт по 3 чётных и 1 нечётному варианту второй цифры, из которых первые три- каждый даёт по 2 варианта для 3ей цифры, а оставшийся один- даёт 3 варианта для 3ей цифры.
То есть получаем: 2 * ( 3*2 + 1*3 ) = 18 вариантов, если первая цифра- чётная.
Итого, можно составить: 12 + 18 = 30 разных трёхзначных чисел