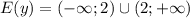1.
то что показано как решать неэффективно
x² + y² + 2y - 9 = 0
3x - y - 1 = 0
y² + 2y + 1 + x² - 10 = 0 (1)
y = 3x - 1 (2)
(y + 1)² + x² = 10 и подставляем из (2)
(3x - 1 + 1)² + x² = 10
9x² + x² = 10
x² = 1
x = ± 1
x = 1 y = 3x - 1 = 2
x = -1 y=3x - 1 = -4
ответ (1, 2) (-1, -4)
2)
x² - 4x - 5 < 0
3x - 9 > 0
разложим на множители x² - 4x - 5 = (x - 5)(x + 1)
D = 16 + 20 = 36
x12 = (4 +- 6)/2 = 5 -1
(x + 1)(x - 5) < 0
3(x - 3) > 0
Применяем метод интервалов
(-1) (5)
(3)
x ∈ (-1, 5) ∩ (3, +∞)
ответ x ∈ (3, 5)
3)
подкоренные выражения ≥ 0
x - 3 ≥ 0
x² -7x + 6 ≥ 0
раскладываем второе
D = 49 - 24 = 25
x12 = (7 +- 5)/2 = 6 1
x² -7x + 6 = (x - 1)(x - 6)
Применяем метод интервалов
[1] [6]
[3]
x ∈ {(-∞, 1] U [6, +∞)) ∩ (3, +∞)
ответ x ∈ [6, +∞)
Функция y = cosx изменяется в пределах от -1 до 1. Оценим в виде двойного неравенства
Множество значений функции![E(y)=[-6;-4]](/tpl/images/0075/1551/24d96.png)
Множество значений функции sin 2x - [-1;1]. Аналогично, оцениваем в виде двойного неравенства
Множество значений функции:![E(y)=[0;2].](/tpl/images/0075/1551/6a953.png)
Графиком функции является гипербола. Переходя к пределу при х стремящихся к бесконечности горизонтальная асимптота функции
Область значений функции :