Объяснение:
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
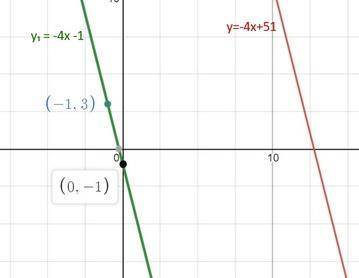
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1

2) 6b + 12 - b^2 - 2b = 12 - b^2 + 4b
3) ax - 7x + 2a - 14
4) 6y - 15 - 6y^2 + 15y
5) 3a^2 - 2a + 12a - 8 = 3a^2 + 10a - 8
1) (3x^2 + 5)(6x^2 - 1) = 18x^4 - 3x^2 + 30x^2 - 5 = 18x^4 + 27x^2 - 5
2) (3c^2 - 2c + 4 (c - 2) = 3c^3 - 6c^2 - 2c^2 + 4c + 4c - 8 =
= 3c^3 - 8c^2 + 8c - 8
3) (y^2 - 5)(y^2 + 5) = y^4 - 25
4) (a + 4)(a^2 - 9a - 3) = a^3 - 9a^2 - 3a + 4a^2 - 36a - 12 =
= a^3 - 5a^2 - 39a - 12
5) (x^2 + 4)(x - 3) = x^3 - 3x^2 + 4x - 12