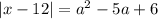
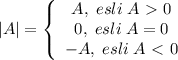
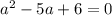 при
при 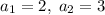 .
.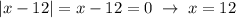 .
.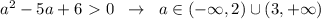
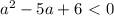 , то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае
, то решений уравнение не будет иметь,так как модуль не может принимать отрицательные значения. Это будет в случае 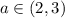 .
.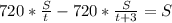 - на S сокращаем
- на S сокращаем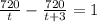
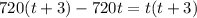
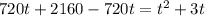
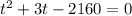
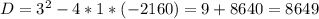
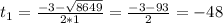 - не подходит. время не может быть отрицательным
- не подходит. время не может быть отрицательным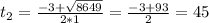 с - время, за которое проходит круг 1-й велосипедист
с - время, за которое проходит круг 1-й велосипедист