* * * * * * * * * * * * * * * * * * * * * * * *
Найдите площадь фигуры с ограниченной линиями
y=x³ , y =1 , x= 2 (постройте график)
ответ: 2,75 кв. ед.
Объяснение:
Найдем точки пересечения графиков функций y=x³ и y=1 :
1 = x³ ⇒ x =1 (1 ; 1) * * * a =1 * * *
* * *x³ -1 =0 ⇔(x -1)(x²+x+1) =0 ⇔[ x -1=0 ; x²+x+1 =0 .⇒ x=1. * * * * * * x²+x+1 =0 не имеет действительных корней * * *
-----------------------------------------------------------
Построить схематический график нечетной функции y = x³ нетрудно (кубическая парабола).
y =1 → линия параллельная оси абсцисс ( x)
x=2 → линия параллельная оси ординат (y)
-----------------------------------------------------------
S = ₁ ∫² (x³ -1 )dx ( пределы интегрирования: a=1 нижний , b=2 верхний)
* * * Формула Ньютона – Лейбница * * *
S = ( x⁴ /4 -x ) | ₁ ² = (2⁴ /4 -2) - (1⁴ /4 -1) = 2 +3/4 =2,75 (кв. ед.)
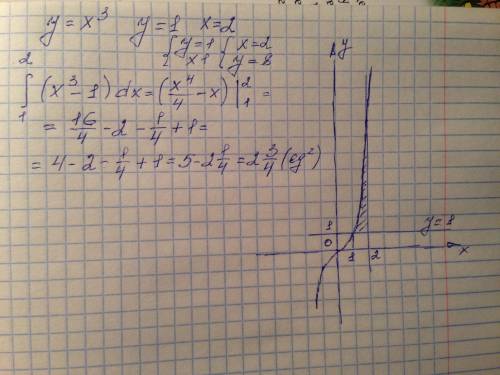
a) х^2 + xy - x - ax + a - a = x^2+ xy - x - ax = x( x + y ) - x( 1 + a )
b) x^2 - 3x -x + 3 +3x -5 = x^2 - x - 2
d = 1 + 4*2 = 9
x_1 = (1 - 9) / 2 = -2 / 2 = -1
x_2 = (1 + 3) / 2 = 4 / 2 = 2
√2*x=√2
sin nx=n cos nx
sin2x=2 cos 2x