Дано: прямоугольный Δ
a; b - катеты
S=90 см²
S₁+S₂ = а²+b² =369 см₂
a-? b-?
Решение
1) Первое уравнение получаем из условия:
а²+b² = 369
2) Площадь прямоугольного треугольника равна половине произведения катетов, получаем второе уравнение:
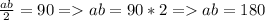
3) Решаем систему: (a>0; b>0)
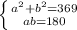
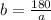
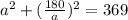
a≠0
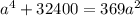
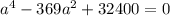
Замена: а²=t ( t > 0)
Решаем уравнение:
t² - 369t + 32400 = 0
D = 369² - 4·1·32400 = 136161 - 129600 = 6561 = 81²
t₁ = (369-81)/2 = 144
t₂ = (369+81)/2 = 225
Обратная замена:
При t₁ = 144 => a² = 144 => a₁ = - √144 = - 12 < 0
a₂ = √144 = 12 > 0
При t₂ = 225 => a² = 225 => a₃ = - √225 = - 15 < 0
a₄ = √225 = 15 > 0
Зная а₁=12 и а₂ = 15, найдем b
b₁ = 180/12 = 15
b₂ = 180/15 = 12
Получаем два решения взаимозаменяемых:
а=12; b=15
а=15; b=12
ответ: 12 см; 15 см - катеты
5x-9x=-4-4
-4x=-8
X=-8:-4
X=2
ответ :2