Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
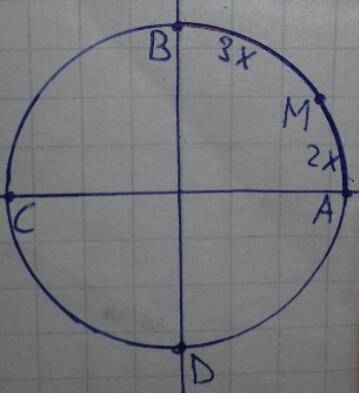
∪AC = π = 2·∪AB ⇒ ∪AB = 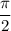
Пусть ∪AM =  , тогда ∪MB =
, тогда ∪MB = 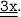
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x = 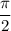 ⇒
⇒
x = 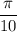 ⇒
⇒ 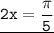 ;
; 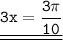
∪DM = ∪DA + ∪AM = 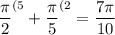
∪MC = ∪MB + ∪BC = 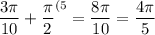
ответ: длина ∪AM = 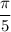
длина ∪MB = 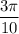
длина ∪DM = 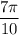
длина ∪MC = 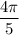
Пусть х - первое число, у - второе число.
1,2х - первое число после его увеличения на 20%;
1,4у - второе число после его увеличения на 40%
Т.к. их первоначальная сумма была 200, а потом стала 256 получаем систему уравнений:
х + у = 200
1,2х + 1,4у = 256
выразив в впервом х: х = 200 - у и подставив во второе получим:
1,2 (200 - у) + 1,4у = 256
240 - 1,2у + 1,4 у = 256
0,2 у = 256 - 240
0,2у = 16
у = 80
х = 200 - 80 = 120.
ответ.
120 - первое число,
80 - второе число.
1,2 * 120 = 144 - первое число после его увеличения на 20%;
1,4 + 80 = 112 - второе число после его увеличения на 40%