Решение системы уравнения v=3; u=2.
Объяснение:
Решить систему уравнений:
2u-v=1
3u+2v=12 методом сложения
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
В данной системе нужно первое уравнение умножить на 2:
4u-2v=2
3u+2v=12
Складываем уравнения:
4u+3u-2v+2v=2+12
7u=14
u=2
Теперь подставляем значение u в любое из двух уравнений системы и вычисляем v:
2u-v=1
-v=1-2u
v=2u-1
v=2*2-1
v=3
Решение системы уравнения v=3; u=2.
1) 
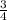∉ Z
2) <
3) 0.12
4) А = 3 , В = 7 , с = 7 , 2 вариант записи
Объяснение:
N - множество натуральных чисел: 1,2,3,4,5,6,...
Z - множество целых чисел: ...-4,-3,-2,-1,0,1,2,3,4,...
Q - множество рациональных чисел, т.е множество дробей.
∈ - знак принадлежности какого-то элемента какому-то множеству, например 3 ∈ N - 3 принадлежит множеству N
∉ - знак непринадлежности - например -8 ∉ N - -8 не принадлежит множеству N
1) 3/4 не принадлежит целым числам
не принадлежит - знак ∉, целым числам - Z
отсюда ответ - 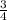∉ Z
2) Сравнить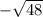 
и 58
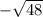- отрицательное число, о 58 - положительное, тогда необходим знак < :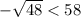 
3) Вычислить значение корня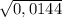 
Какое число нужно возвести в квадрат, чтобы получить 0.0144?
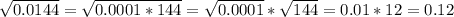
4) Сократить дробь.
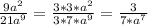- сократили и записали в виде 
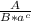, где А = 3, В = 7, с = 7
x1+x2=-b/a=-8
x1x2=c/a=-10