(1;3)
Объяснение:
1) Метод алгебраического сложения
{х+у=4 умножаем на (-2)
2х-у=5
{-2х-2у=-8
2х-у=5
Складываем уравнения
-3у=-3 умножаем на (-1)
у=3/3
у=1
Подставляем значение в одно из уравнений
х+у=4
х+1=4
х=4-1
х=3
ответ: (1;3)
2) Метод Подстановки
{х+у=4
2х-у=5
{х=4-у
2х-у=5
Подставляем значение х первого уравнения, во второе
2х-у=8
2(4-у)-у=5
8-2у-у=5
8-3у=5
-3у=5-8
-3у=-3
у=3/3
у=1
Подставляем значение у в первое уравнение
х=4-у
х=4-1
х=3
ответ: (1;3)
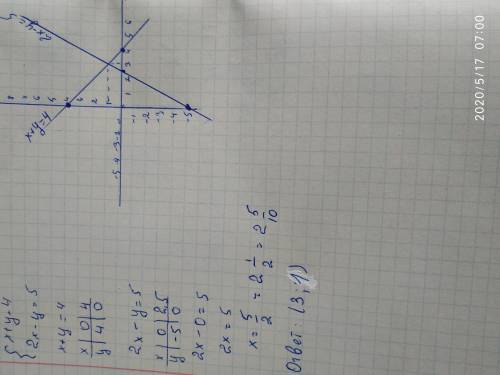
3) Графический
{х+у=4
2х-у=5
Берём первое уравнение
х+у=4
Пусть х будет 0, тогда у будет равно
0+у=4
у=4
Первая координата нашей прямой (0;4)
Пусть у будет 0, тогда х будет...
х+0=4
х=4
Вторая координата нашей прямой
(4;0)
Строим прямую в прямоугольной координатной плоскости, с координатами
(0;4) (4;0)
Берём второе уравнение
2х-у=5
Пусть х будет 0, тогда у будет равно
2*0-у=5
-у=5
у=-5
Первая координата нашей прямой (0;-5)
Пусть у будет равно 0, тогда х будет...
2х-0=5
2х=5
х=5/2
х=2целых1/2
х=2,5
Вторая координата прямой (2,5;0)
Строим прямую, в прямоугольной координатной плоскости, с координатами (0;-5) (2,5;0)
Точкой пересечения двух прямых, будет решением для данной системы уравнений
Координаты пересечения двух прямых является (1;3)
ответ: (1;3)
Стандартные решения через дискриминант уже написаны, можно по ним свериться. Предложу "быстрые", но которые не всегда срабатывают.
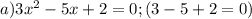- видно, что сумма коэффициентов в этом квадратном уравнении равна 0. Корни находятся быстро и безболезненно.
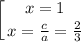
ответ: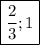 
б) тут действительно проще всего выделить полный квадрат. С опытом приходит их видение.
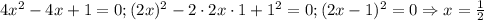
ответ: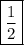 
в)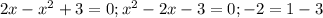 
Здесь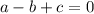 
или проще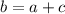 
В этом случае
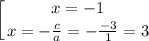
ответ: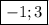 
P.S. как видим, ни разу не был вычислен дискриминант. И примеров таких уравнений довольно много, в том числе и на экзаменах. Поэтому советую запомнить эти частные случаи и тренироваться побольше.
Формула нахождения корней квадратного уравнения: (-b ±√D) / 2 * a
Предположим, чтобы получить нужные корни, будет 2 варианта: -8/4 и -2/4. Отсюда a = 2; √D = 3 => D = 9; b = 5
Получаем 2x² + 5x + c = 0
Нужно найти с. Его мы находим из формулы нахождения дискриминанта D = b² - 4ac
9 = 25 - 4 * 2 * c
Получаем, что c = 2
2x² + 5x + 2 = 0