Первая встреча Гринева и Пугачева («Капитанская дочка») происходит в момент поездки Петра в Оренбург на службу. В тот день за окном стоял сильный буран, из-за которого Гринев и его слуга теряют путь и не знают, куда ехать дальше. Пугачев на тот период является еще неизвестным человеком и представляется «вожатым». Он встречается с Петром и показывает верную дорогу. Чтобы как-то отблагодарить человека, Гринев дарит ему свой теплый красивый тулуп.
Вторая встреча двух героев происходит в Белогорской крепости в момент, когда Гринев проходит службу. Пугачевские воины осаждают крепость. В тот момент Петр узнает в Пугачеве того самого «вожатого», которому он когда-то подарил тулуп за указанный верный путь. Гриневу поступает предложение перейти на сторону Пугачева, но тот отказывается, так как является верным и преданным присяге императрице. Уважая такой смелый жест, мужественность и высокоморальность, Петру дается возможность уехать из крепости целым и невредимым.
Третья встреча героев – в Оренбурге. Петр Гринев едет в крепость, чтобы возлюбленную девушку, а Пугачев ему в освобождении Маши от Швабрина. Молодые уезжают из Белогорской крепости.
Последняя встреча персонажей происходит во время Пугачевской казни на плацу, когда герои произведения встречаются взглядами. Гринев кивает головой в сторону Пугачева, они в течение минуты смотрят друг на друга, а затем происходит казнь.
Теорема (о сумме углов выпуклого многоугольника)
Сумма внутренних углов выпуклого многоугольника равна 180º(n-2). (n — количество сторон многоугольника).
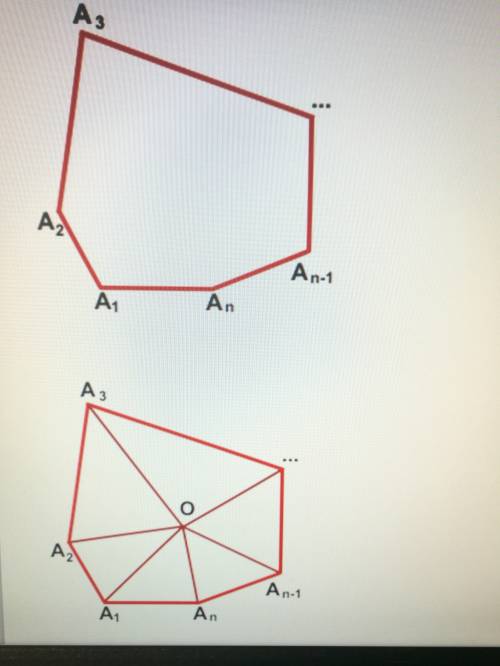
(смотри верхний рисунок)
— выпуклый n -угольник.
Обозначим внутри многоугольника произвольную точку O.
Соединим точку O с вершинами многоугольника.
(смотри нижний рисунок)
Получили n треугольников.
Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.
То есть в данном случае у нас 6-угольник, имеем 6 треугольников, сумма углов которых 6*180 и минус 2*180 – сумма углов при вершине. Получается 180*(6 – 2) = 720 гр.
Так как сумма углов при вершине O составляет 360º, то сумма углов многоугольника равна сумме углов n треугольников минус 360º.
3x + 2y = -1;
x2 + x(-(1 + 3x)/2)= 9 - 3 * ((1 + 3x)/2);
y = - (1 + 3x)/ 2;
x2 - (x - 3x2)/2 = 9 - (3 - 9x)/2; | *2;
2x2 - x - 3x2 = 18 - 3 -9x;
x2 + 8x - 15 = 0;
D = 64 - 60 = 4;
x1 = (8 + 2)/ 2 = 5;
x2 = (8 - 2)/2 = 3;
y1 = (-1 - 3*5)/2 = - 8;
y2 = (- 1 - 9)/2 = -5;