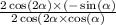
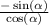
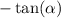
y₁ = x² - 4x + 3; y₂ = x - 1
исследуем функцию y₁ = x² - 4x + 3
Нули функции:
x² - 4x + 3 = 0
D = 16 - 12 = 4
√D = 2
x₁ = (4 - 2):2 = 1
x₂ = (4 + 2):2 = 3
Вершина параболы: х = 4/2 = 2
у(2) = 4 - 4·2 + 3 = -1
Для определения пределов интегрирования найдёи точки пересечения функций
y₁ = x² - 4x + 3 и y₂ = x - 1
x² - 4x + 3 = х - 1
x² - 5x + 4 = 0
D = 25 - 16 = 9
√D = 3
x₁ = (5 - 3):2 = 1
x₂ = (5 + 3):2 = 4
Итак, нижний предел интегрирования x₁ = 1, верхний - x₂ = 4
Поскольку на интервале х∈(1,4) у₂ > у₁, то будем находить интеграл от разности
у₂ - у₁ = x - 1 - (x² - 4x + 3) = x - 1- x² + 4x - 3 = - x² + 5x - 4
∫(- x² + 5x - 4)dx = -x³/3 + 5x²/2 - 4x
Подставим пределы интегрирования
S = (-64/3 + 5·16/2 - 4·4) - (-1/3 + 5/2 - 4) = -64/3 + 40 - 16 +1/3 - 5/2 + 4 =
= - 21 + 28 - 2,5 = 4,5
1)=8а²(в²-9с²)=8а²(в-3с)(в+3с).
2)=2(х²-12ху+36у²)=2(х-6у)².
3)=-2а(4а4-4а²+1)= -2а(2а²-1)².
4)=5(а³-8в6)=5(а³-(2в²)³)=5(а-2в²)(а²+2ав²+4в4)
5)=(а³+а²)-(ав-а²в)=а²(а+1)-ав(1+а)=(а+1)(а²-ав)=а(а+1)(а-в)
6)=с4(а-1)-с²(а-1)=(а-1)(с4-с²)=с²(а-1)(с²-1)=с²(а-1)(с-1)(с+1).
1)=(х-у)²-7²=(х-у-7)(х-у+7)
2)=а²-(3в-с)²=(а+3в-с)(а-3в+с)
3)=(в³)²-(2в²-3)²=(в³+2в²-3)(в³-2в²+3).
4)=(m³+3³n³)+(m+3n)²=(m+3n)(m²-3mn+9n²)+(m+3n)²=(m+3n)(m²-3mn+9n²+m+3n).
5)=x²-y²+2x+4y-3=(x²+2x+1)-(y²-4y+4)=(x+1)²-(y-2)²=(x+y-1)(x-y+3).