2)Пусть х - число роз в первом букете первоначально, тогда во втором букете их было первоначально - 4х. К первому букету добавили 15 роз, то количество роз в первом букете стало х+15. Ко второму добавили 3 розы, тогда во втором букете их стало 4х+3. Т.к. в обоих букетах роз стало поровну, значит букеты разрешается приравнять:
х+15=4х+3
х=4 (розы) - было в первом букете первоначально
4х=4*4=16(роз) - было во втором букете первоначально
ответ:4, 16.
3)
х - одно число, y- другое число
Составим систему:
x+y=138
2/9x=80/100y
x+y=138
2/9x=4/5y
x+y=138
5x=18y
x=138-y
5*(138-y)=18y
x=138-y
690=23y
x=138-y=138-30=108
y=30
ответ:30, 108.
Правая часть уравнения должна быть неотрицательной:
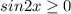
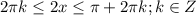
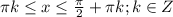
То есть первая и третья четверти,где синус и косинус одного знака.
Очевидно,что модуль их суммы будет больше единицы всегда(неравенство треугольника,где в качестве третьей стороны выступает радиус единичной окружности)
Рассмотрим выражение под модулем:
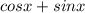
Попробуем найти максимум такой функции
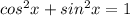
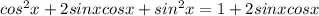
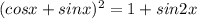
Очевидно,что левая часть принимает наибольшее значение,когда таковое принимает правая.
Правая часть принимает наибольшее значение при
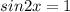
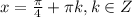
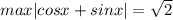
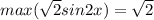
Разделим обе части уравнения на 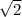
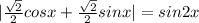
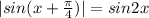
Очевидно,что синус в первой четверти(для третьей аналогично,так как модуль) больше тогда,когда больше аргумент.
Рассмотрим аргументы обоих синусов на полуинтервале:
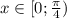
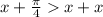
Значит: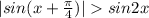
Рассмотрим аргументы обоих синусов на полуинтервале:
На этом промежутке происходит переход во вторую четверть,где с точностью до наоборот синус большего аргумента имеет меньшее значение.
![x \in (\frac{\pi}{4};\frac{\pi}{2}]](/tpl/images/0101/3655/1d186.png)
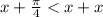
Значит: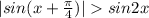
Очевидно,что единственным решением уравнения является:
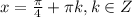
1) F' = 3x^2 - 9 = 0
3x^2 = 9, x^2 = 3, x= +-√3
2) F' = 2/(x^2) = 0 - нет таких точек, чтобы производная была равна 0, но есть точка, в которой производной не существует, а именно: х=0