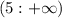lim((2x²/x²+15x/x²+25/x²)/(x²/x²+15x/x²+50/x²))= x->∞ =lim((2+15/x+25/x²)/(1+15/x+50/x²)=2/1=2 x->∞ величинами 15/x, 25/x², 50/x² можно пренебречь, т.к при x->∞ их значение ->0. они бесконечно малы
- квадратичная функция. График парабола => Сначала находим вершину. Пусть А(m;n) - вершина параболы => m=-b/2a=(-4)/(-4)=1 => n=-2+4+6=8=> вершина параболы находится в точке с координатами: (1;8). Остальные точки находим подставляя в функцию вместо х: 2 и 0, 3 и -1, 4 и -2 и т.д. 1)При х=-2 у=-10; при х=0 у=6; при х=3 у=0 2)При у=10 х=-2; при у=6 х=0; при у=0 х=3 3)у наиб=n (в вершине) =8 4) Возрастает (большему значению х соответствует большее значение у) на промежутке (-∞;1]; убывает (большему значению х соответствует меньшее значение у) на промежутке [1;+∞) 5)Аргумент - х. При у=0 х=-1 и 3=> y>0 при х∈(-1;3) y<0 при x∈(-∞;-1)U(3;+∞)
а)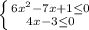
Строим координатную прямую и отмечаем на ней закрашенными точками 1\6 и 1
Получается, что х принадлежит [1\6;1]
Снова строим координатную прямую и отмечаем на неё закрашенную точку 3\4. Получаем, что х принадлежит![(-\infty;\frac{3}{4}]](/tpl/images/0077/2198/d1207.png)
3) Общий
Отмечаем на координатной прямой все точки 1\6, 3\4 и 1.
Совмещаем графики и получаем решение системы уравнений.
x принадлежит [1\6;\3\4]
Напоминаю, что вид скобок имеет значение.
б)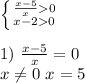
Строим координатную прямую и отмечаем на ней выколотые точки 0 и 5. х принадлежит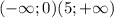
2) х>2
Строем координатную прямую с выколотой точкой 2 и получаем, что х принадлежит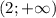
Объединяем значения на координатной прямой и получаем решение системы уравнений. х принадлежит