1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:
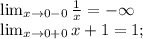
Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).
Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как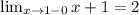 
При x=1 ⇒y=2.
Подставим координаты (1;2) в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: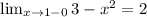 
Действительно 2=2, значит функция не будет являться непрерывной в точке 1.
ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1
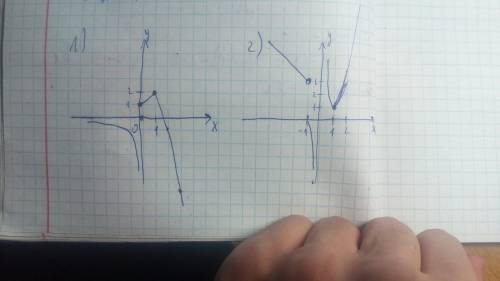
2) Аналогично:
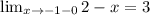
3≠-1, значит -1- это точка разрыва.
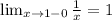
В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.
Проверим: 
.
Так как точка х=0 лежит в области определения функции 
, а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
ответ: х=-1 - точка разрыва, х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1
опытаемся найти точки их пересечения, решив систему:
(x-2) 2 + (y-3) 2=16
(x-2) 2 + (y-2) 2=4
(x-2) 2=16 - (y-3) 2
(x-2) 2=4 - (y-2) 2,
отсюда 16 - (y-3) 2=4 - (y-2) 2
16-у2+6 у-9=4-у2+4 у-4 ещё
6 у-4 у=4-4+9-16 ещё
2 у=-7 найдём игрек
у=-3,5 и попробуем найти икс
(x-2) 2=4 - (-3,5-2) 2
(x-2) 2=4-30,25
(x-2) 2=-25,75, а квадрат не может быть отрицательным, следовательно, эти две окружности не пересекаются. центры окружностей - в точках (2; 3) и (2; 2) соответственно, то есть расстояние между центрами равно единице, а радиусы - 4 и 2, то есть вторая, меньшая, окружность расположена внутри первой.
ответ: малая окружность расположена внутри большой.
