а) 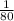
б) 324
Объяснение:
а) 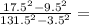
И числитель и знаменатель это формула сокращенного умножения, а точнее разница квадратов. Раскладывается следующим образом:
a² - b² = (a - b) × (a + b)
Сначала разберемся с числителем:
1) 17.5² - 9.5² = (17.5 - 9.5) × (17.5 - 9.5)
2) (17.5 - 9.5) × (17.5 - 9.5) = (8) × (27); (в конце скобки писать не обязательно, это я для наглядности)
Так и оставим пока что. Далее действия со знаменателем:
1) 131.5² - 3.5² = (131.5 - 3.5) × (131.5 + 3.5)
2) (131.5 - 3.5) × (131.5 + 3.5) = (128) × (135); (в конце скобки писать не обязательно, это я для наглядности)
Подставляем числитель и знаменатель:
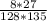
8 и 128 сокращаются. Так же 27 и 135 сокращаются:
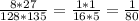
б) 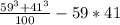
В числителе находится формула сокращенного умножения, а точнее сумма кубов. Раскладывается следующим образом:
а³ + b³ = (a + b) × (a² - ab + b³)
Разберемся с числителем:
1) 59³ + 43³ = (59 + 41) × (59² - 59 × 41 + 41²)
2) (59 + 41) × (59² - 59 × 41 + 41²) = (100) × (59² - 59 × 41 + 41²)
Так пока и оставим (100 не обязательно брать в скобки, это я для наглядности).
Поставим получившийся пример обратно в числитель:
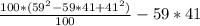
100 и 100 сокращаются:
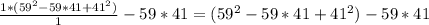
59² - 59 × 41 + 41² - 59 × 41 = 59² + 41² - 59 × 41 - 59 × 41 (от перемены мест слагаемых сумма не изменяется)
59² + 41² - 59 × 41 - 59 × 41 = 59² - 2 (59 × 41) + 41²
Это разложенный вид формули сокращенного умножения, а точнее квадрата разницы. Складывается следующим образом:
a² - 2ab + b² = (a - b)²
59² - 2 (59 × 41) + 41² = (59 - 41)² = 18² = 324
Пример 1. В урне 10 белых и 8 черных шаров. Наудачу отобраны 5 шаров. Найти вероятность того, что среди них окажется ровно 2 белых шара.
Подставляем в формулу (1) значения: K=10K=10, N−K=8N−K=8, итого N=10+8=18N=10+8=18, выбираем n=5n=5 шаров, из них должно быть k=2k=2 белых и соответственно, n−k=5−2=3n−k=5−2=3 черных. Получаем:
P=C210⋅C38C518=45⋅568568=517=0.294.P=C102⋅C83C185=45⋅568568=517=0.294.
Пример 2. В урне 5 белых и 5 красных шаров. Какова вероятность вытащить наудачу оба белых шара?
Здесь шары не черные и белые, а красные и белые. Но это совсем не влияет на ход решения и ответ.
Подставляем в формулу (1) значения: K=5K=5 (белых шаров), N−K=5N−K=5 (красных шаров), итого N=5+5=10N=5+5=10 (всего шаров в урне), выбираем n=2n=2 шара, из них должно быть k=2k=2 белых и соответственно, n−k=2−2=0n−k=2−2=0 красных. Получаем:
P=C25⋅C05C210=10⋅145=29=0.222.P=C52⋅C50C102=10⋅145=29=0.222.
Пример 3. В корзине лежат 4 белых и 2 черных шара. Из корзины достали 2 шара. Какова вероятность, что они одного цвета?
Здесь задача немного усложняется, и решим мы ее по шагам. Введем искомое событие
A=A= (Выбранные шары одного цвета) = (Выбрано или 2 белых, или 2 черных шара).
Представим это событие как сумму двух несовместных событий: A=A1+A2A=A1+A2, где
A1=A1= (Выбраны 2 белых шара),
4х=8
х=2
ответ:При х=2