а) c+d+3x(c+d) = (c+d)(1+3x);
б) 2a+ax+2bx+4b =a(2 + x) + 2b(x + 2) = (x + 2)(a + 2b);
в) mn-3n+3-m = n(m - 3) - (m - 3) = (m - 3)(n - 1);
г) 2cx-3cy+6by-4bc = здесь что то не так списано...
д) x2 (во второй степени) -3ax+6a-2a =здесь что то не так списано...
Разложите на множители: а) a-b+2c(a-b) =(a-b)(1 + 2c);
б) by+3b+2cy+6c =b(y+3) +2c(y+3) = (y+3)(b+2c);
в) kl-5l-k+5 =l(k-5) - (k-5) = (k-5)(l - 1);
г) 3ab-2ac-4cd-6bd =здесь что то не так списано...
д) y2 (во второй степени) -2by+6b-3y =y(y - 2b) -3(y - 2b) = (y - 2b)(y - 3)
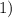
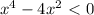

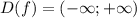
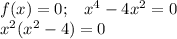



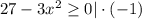
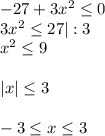
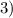
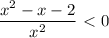
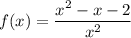
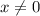
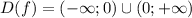
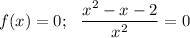

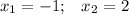
 - решение неравенства
- решение неравенства
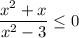


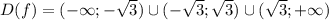

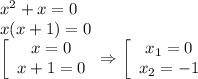
![x \in (- \sqrt{3} ;-1]\cup[0;\sqrt{3} )](/tpl/images/0255/3734/02302.png)
1. Всего двузначных чисел 99 - 9 = 90.
1) Из них нечетных только 45, вероятность того, что он написал число нечетное равна 45/90 = 1/2.
2) Имеем последовательность 12, 15, ... , 99 - арифметическую прогрессию
Т.е. из 90 чисел всего только 30 чисел, кратные трем.
Вероятность того, что он написал число, кратное трем, равна 30/90=1/3
2. Из условия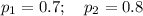
Вероятности промаха каждого стрелка: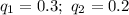 соответственно.
соответственно.
1) Вероятность того, что один из стрелков попал в мишень, равна
2) Вероятность того, что в мишень попал, по крайней мере, один стрелок, равна
3) Вероятность того, что оба стрелка попали в мишень, равна
4) Вероятность того, что оба стрелка промахнулись, равна
5) Вероятность того, что, по крайней мере, один из стрелков промахнулся, равна