В решении.
Объяснение:
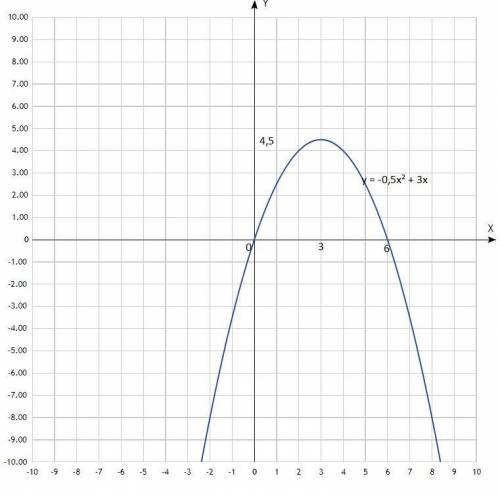
Дана функция у = -1/2 х² + 3х; найти промежуток её убывания.
Построить график функции.
Сначала преобразовать уравнение функции для упрощения.
-1/2 х² + 3х = -0,5х² + 3х, неполное квадратное уравнение.
Приравнять к нулю:
-0,5х² + 3х = 0
0,5х (-х + 6) = 0
0,5х = 0;
х₁ = 0;
-х + 6 = 0
-х = -6
х = 6;
График - парабола, ветви направлены вниз, пересекают ось Ох в точках: х = 0; х = 6 (нули функции).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2 4 6 8
у -8 -3,5 0 2,5 4 4 0 -8
По вычисленным точкам построить параболу.
Согласно графика, функция убывает в промежутке х∈(3; +∞).
Найдем, какую часть бассейна сможет наполнить каждая из труб за один час.
В условии задачи сказано, что первая труба может наполнить бассейн за 3 часа, а вторая труба наполняет весь бассейн за 2 часа, следовательно, за 1 час первая труба сможет наполнить 1/3 часть бассейна, а вторая труба сможет наполнить 1/2 часть бассейна.
Тогда, при совместной работе две трубы за 1 час смогут наполнить 1/2 + 1/3 = 3/6 + 2/6 = 5/6 частей бассейна, а весь бассейн наполнят за 6/5 ч , что в минутах составляет (6/5) * 60 = 6 * 60 / 5 = 6 * 12 = 72 мин.
ответ: за 72 минуты.
В скобках нам даны формулы синуса суммы — в первых скобках и косинуса суммы — во вторых скобках. Применяем эти формулы, затем основное тригонометрическое тождество и получаем:
(sinαcosβ+cosαsinβ)2 + (cosαcosβ-sinαsinβ)2 = sin2(α+β)+cos2(α+β)=1.
*2- это степень( в квадрате тоесть)