Такс, ну я попробую, хз что получится. Я так то в седьмом классе)
2. (пикчу прикрепил)
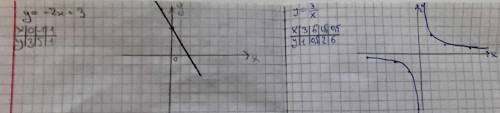
а) Это график обычно линейной функции
б) А это уже график обратной пропорциональности (гипербола)
3.
а) Возводим все в квадрат. 2 переносим.
x + 4 = x^2
Теперь чертим график y = x^2 (парабола) и график y = x + 4 (линейная функция). Точки пересечения - это и есть наши x. Если потом влом не будет, может нарисую.
б) Выносим x
x(x^2 + 2) + 3 = 0
3 переносим, делим все на x
x^2 + 2 = -3/x
Снова чертим график параболы (x^2 + 2) и гиперболы (-3/x). Находим точки пересечения, это и есть значение x. Думаю все это и сам умеешь, но опять же, может потом начерчу.
Напоминаю, что график гиперболы y = -3/x будет проходить в правой верхней (2) четверти и в левой нижней (4)!
4.
Выносим x
x(x + 5)
x ≠ 0 (т.к. на ноль делить нельзя).
x ≠ -5
Любое другое значение нас устраивает.
x ∈ (-∞; -5) v (-5; 0) v (0; +∞)
p.s. Извини, что так долго. Отвлечься пришлось)
Покажу один из сопособов решения таких неравенств
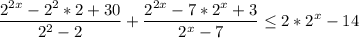
1) проверим ограничения
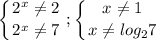
2) введем замену 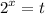
получаем,
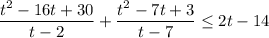
А далее самое интересное
будем делить многочлен на многочлен
_t²-16t+30 | t-2 и _t²-7t+3 | t-7
t²-2t ______ t²-7t _____
_____ t-14 ____ t
_ -14t+30 3 (остаток)
-14t+28
------------
2 (остаток)
тогда
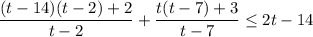
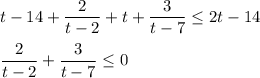
теперь все совсем просто
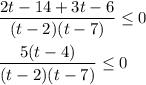
решаем методом интервалов
__-____ 2 ___+____4___-____7___+____
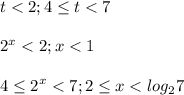
Не забываем проверить ограничение
ответ (-∞; 1)∪[2; log₂7)
-3y=-3
y=1