Правая часть уравнения должна быть неотрицательной:
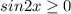
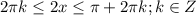
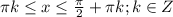
То есть первая и третья четверти,где синус и косинус одного знака.
Очевидно,что модуль их суммы будет больше единицы всегда(неравенство треугольника,где в качестве третьей стороны выступает радиус единичной окружности)
Рассмотрим выражение под модулем:
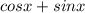
Попробуем найти максимум такой функции
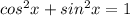
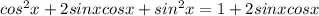
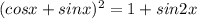
Очевидно,что левая часть принимает наибольшее значение,когда таковое принимает правая.
Правая часть принимает наибольшее значение при
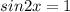
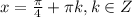
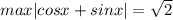
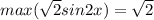
Разделим обе части уравнения на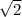 
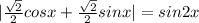
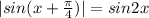
Очевидно,что синус в первой четверти(для третьей аналогично,так как модуль) больше тогда,когда больше аргумент.
Рассмотрим аргументы обоих синусов на полуинтервале:
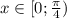
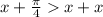
Значит: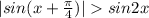
Рассмотрим аргументы обоих синусов на полуинтервале:
На этом промежутке происходит переход во вторую четверть,где с точностью до наоборот синус большего аргумента имеет меньшее значение.
![x \in (\frac{\pi}{4};\frac{\pi}{2}]](/tpl/images/0101/3655/1d186.png)
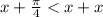
Значит: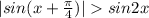
Очевидно,что единственным решением уравнения является:
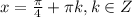
Правая часть уравнения должна быть неотрицательной:
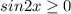
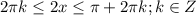
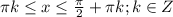
То есть первая и третья четверти,где синус и косинус одного знака.
Очевидно,что модуль их суммы будет больше единицы всегда(неравенство треугольника,где в качестве третьей стороны выступает радиус единичной окружности)
Рассмотрим выражение под модулем:
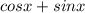
Попробуем найти максимум такой функции
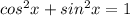
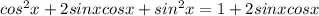
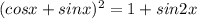
Очевидно,что левая часть принимает наибольшее значение,когда таковое принимает правая.
Правая часть принимает наибольшее значение при
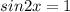
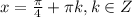
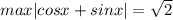
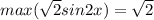
Разделим обе части уравнения на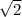
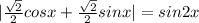
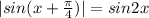
Очевидно,что синус в первой четверти(для третьей аналогично,так как модуль) больше тогда,когда больше аргумент.
Рассмотрим аргументы обоих синусов на полуинтервале:
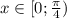
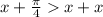
Значит: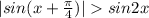
Рассмотрим аргументы обоих синусов на полуинтервале:
На этом промежутке происходит переход во вторую четверть,где с точностью до наоборот синус большего аргумента имеет меньшее значение.
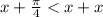
Значит: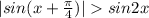
Очевидно,что единственным решением уравнения является:
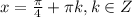
a(3+x) a
2) b² = b
b(b+c) b+c
3) 2(a+2) = 2
(a+2)(a-2) a-2
4) (x+y)(x-y) = x+y
x(x-y) x