Решить систему линейных уравнений методом подстановки и методом сложения:
{
y
+
2
x
=
1
y
−
x
=
3
Решение методом подстановки.
{
y
+
2
x
=
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
y
−
x
=
3
⇒
{
y
=
−
2
x
+
1
(
−
2
x
+
1
)
−
x
=
3
⇒
{
y
=
−
2
x
+
1
−
3
x
−
2
=
0
⇒
{
y
=
−
2
x
+
1
x
=
−
2
3
⇒
{
y
=
7
3
x
=
−
2
3
y
=
2
1
3
;
x
=
−
2
3
Решение методом сложения.
{
y
+
2
x
=
1
y
−
x
=
3
Вычитаем уравнения:
−
{
y
+
2
x
=
1
y
−
x
=
3
(
y
+
2
x
)
−
(
y
−
x
)
=
1
−
3
3
x
=
−
2
x
=
−
2
3
Подставиим найденную переменную в первое уравнение:
(
−
2
3
)
+
2
x
=
1
y
=
7
3
y
=
2
1
3
;
x
=
−
2
3
Объяснение:
На путь из деревни в город, равный 90 км, первый мотоциклист тратит на 18 мин больше, чем второй, поскольку его скорость на 10 км/ч меньше скорости второго. Найдите скорость каждого мотоциклиста.
Объяснение:
Пусть х км/ч - скорость первого мотоциклиста, тогда (х + 10) км/ч - скорость второго мотоциклиста.
Время в пути первого мотоциклиста равно: 90/х.
Время в пути второго мотоциклиста равно: 90/(х + 10).
18 мин = 0,3 ч
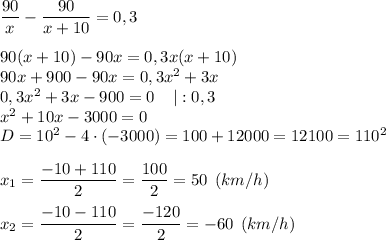
Второй корень не подходит, значит, скорость первого мотоциклиста равна 50 км/ч.
Скорость второго мотоциклиста равна:
50 + 10 = 60 (км/ч)
ответ: 50 км/ч - скорость 1-ого мотоциклиста;
60 км/ч - скорость 2-ого мотоциклиста.