Нужно сравнить длины сторон треугольников
Для этого находим их по формуле расстояния между двумя точками
d=√((x2-x1)^2+(y2-y1)^2)
a)
AB=√((2+2)^2+(-1+1)^2)=√(16)=4
BC=√((-2-2)^2+(1+1)^2)=√(16+4)=√20
CA=√((-2+2)^2+(-1-1)^2)=√(4)=2
Стороны не равны, но сторона BC больше остальных, поэтому проверим выполняется ли на них теорема пифагора
(√20)^2=2^2+4^2
20=4+16
20=20
Теорема Пифагора выполняется, значит треугольник прямоугольный.
б)
AB=√((2+2)^2+(-2+2)^2)=√(16)=4
BC=√((0-2)^2+(1+2)^2)=√(4+9)=√13
CA=√((-2-0)^2+(-2-1)^2)=√(4+9)=√13
т.к. равны 2 стороны, то треугольник равнобедренный.
y=11+6√x-2x√x D(f)=x∈(0:+∞)
2x√x=2*x¹*x¹/₂=2*x³/²
6√x=6*x¹/²
f(x)=-2*x³/²+6*x¹/²+11
(2*x³/²)`=3*x¹/²=3√x
(6*x¹/²)`=3/x¹/²=3/√x
(11)`=0
f`(x)=-3√x+3/√x
Приравниваем производную к нулю:
-3√x+3/√x=0
-3√x*√х+3=0
-3х+3=0
-3х=-3
х=1 - критическая точка.
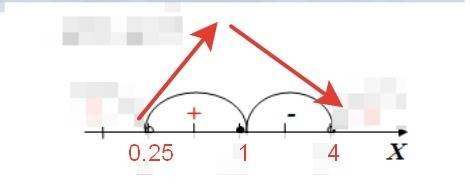
Чтобы узнать, достигает ли функция максимума в точке экстремума х=1, нужно определить знаки производной методом интервалов (рисунок во вложении):
f`(1)=0
f`(0.25)=-3√0.25+3/√0.25=4.5>0 - функция возрастает на отрезке (0;1)
f`(4)=-3√4+3/√4=-4.5<0 - функция убывает на отрезке (1;+∞)
При переходе через точку х=1 производная меняет знак с "+" на "-", значит х=1 - точка максимума функции.
5х=0
х=0