Алгебра: Sin^2 x/2 - cos^2 x/2 = cos2x решить

Sin^2 x/2 - cos^2 x/2 = cos2x решить

👇

Увидеть ответ

Ответ:

Пень01

17.06.2022

-(cos^2(x/2) - sin^2(x/2)) = cos(2x)
-cos(2x) - cos(2x) = 0
-2cos(2x) = 0
cos(2x) = 0
2x = π/2 + πk
x = π/4 + πk/2

4,8(82 оценок)

Открыть все ответы

Ответ:

Nessmikk13

17.06.2022

ОДЗ:

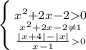
$\left \{ {{x^2+2x-20} \atop{ {x^2+2x-2\neq1 }\atop{\frac{|x+4|-|x|}{x-1}0 }} \right.$

Решаем каждое неравенство:

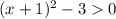x^2+2x-20 ⇒ (x+1)^2-3 0 ⇒ $(x+1-\sqrt{3})(x+1+\sqrt{3})0$

$x\in (-\infty;-1-\sqrt{3}) \cup{-1+\sqrt{3};+\infty)$

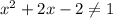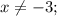
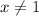
$x^2+2x-2\neq 1$ ⇒ $x^2+2x-3\neq 0$ ⇒ $x\neq -3;$ $x\neq 1$

$\frac{|x+4|-|x|}{x-1}0$

Подмодульные выражения обращаются в 0 в точках

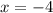x=-4 и x=0

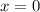
Это точки делят числовую прямую на три промежутка.

Раскрываем знак модуля на промежутках:

(-∞;-4]

|x+4|=-x-4

|x|=-x

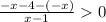$\frac{-x-4-(-x)}{x-1}0$ ⇒ $\frac{-4}{x-1}0$ ⇒ x < 1

решение неравенства (-∞;-4]

(-4;0]

|x+4|=x+4

|x|=-x

$\frac{x+4-(-x)}{x-1}0$ ⇒ $\frac{2x+4}{x-1}0$ ⇒ x < -2 или x > 1

решение неравенства (-4;-2)

(0;+∞)

|x+4|=x+4

|x|=x

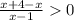$\frac{x+4-x}{x-1}0$ ⇒ $\frac{4}{x-1}0$ ⇒ x > 1

решение неравенства (1;+∞]

Объединяем ответы трех случаев:

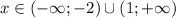
$\frac{|x+4|-|x|}{x-1}0$ при $x \in (-\infty;-2)\cup(1;+\infty)$

ОДЗ:

$\left \{ {{x\in (-\infty;-1-\sqrt{3}) \cup{-1+\sqrt{3};+\infty)} \atop{ {x\neq-3; x\neq 1 }\atop{ x \in (-\infty;-2)\cup(1;+\infty)}} \right.$

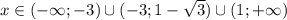
$x\in (-\infty;-3)\cup(-3;1-\sqrt{3}) \cup(1;+\infty)$

Решаем неравенство: 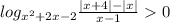$log_{x^2+2x-2}\frac{|x+4|-|x|}{x-1}0$

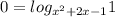
$0=log_{x^2+2x-1}1$

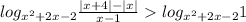
$log_{x^2+2x-2}\frac{|x+4|-|x|}{x-1}log_{x^2+2x-2}1$

Два случая:

если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента

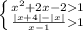$\left \{ {{x^2+2x-21} \atop {\frac{|x+4|-|x|}{x-1}1}} \right.$ ⇒ $\left \{ {{x^2+2x-30} \atop {\frac{|x+4|-|x|-x+1}{x-1}0}} \right.$ ⇒ $\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.$

второе неравенство решаем на промежутках так:

(-∞;-4]

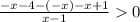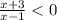$\frac{-x-4-(-x)-x+1}{x-1}0$ ⇒ $\frac{-3-x}{x-1}0$ ⇒ $\frac{x+3}{x-1}$ ⇒ (-3;-1)

не принадлежат (-∞;-4]

на (-4;0]

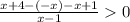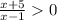$\frac{x+4-(-x)-x+1}{x-1}0$ ⇒ $\frac{x+5}{x-1}0$ ⇒ x < -5 или x > 1

не принадлежат (-4;0]

(0;+∞)

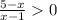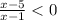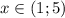
$\frac{x+4-x-x+1}{x-1}0$ ⇒ $\frac{5-x}{x-1}0$ ⇒ $\frac{x-5}{x-1}$ ⇒ $x\in (1;5)$

о т в е т этого случая (1;5)

если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента

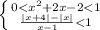$\left \{ {{0$ ⇒ $\left \{ {0$ ⇒ $\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.$

второе неравенство решаем на промежутках так:

(-∞;-4]

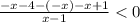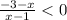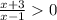$\frac{-x-4-(-x)-x+1}{x-1}$ ⇒ $\frac{-3-x}{x-1}$ ⇒ $\frac{x+3}{x-1}0$ ⇒

(-∞;-3)U(1;+∞)

о т в е т. (-∞;-4]

на (-4;0]

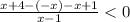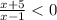$\frac{x+4-(-x)-x+1}{x-1}$ ⇒ $\frac{x+5}{x-1}$ ⇒ -5 < x < 1

о т в е т. (-4;0]

(0;+∞)

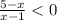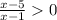$\frac{x+4-x-x+1}{x-1}$ ⇒ $\frac{5-x}{x-1}$ ⇒ $\frac{x-5}{x-1}0$ ⇒ $x\in (0;1)\cup(5;+\infty)$

о т в е т этого случая $(-3;-1-\sqrt{3})$

С учетом ОДЗ получаем окончательный ответ: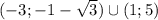 $(-3;-1-\sqrt{3})\cup(1;5)$

4,6(75 оценок)

Ответ:

leoni008p08nm5

17.06.2022

Сказка «Снежная королева» была написана в 1844 г. и опубликована в сборнике «Новые сказки» (1845). Сборник очень удачно появился 21 декабря, накануне Рождества.

В разгаре был роман Андерсена с Дженни (Йенни) Линд. Хотя трудно назвать романтические отношения романом: Линд называла Андерсена братцем. Образ холодной певицы, не отвечавшей Андерсену взаимностью и через 10 лет после знакомства вышедшей замуж за известного композитора, как считают биографы, лёг в основу образа Снежной королевы. С другой стороны, идеальная братская любовь отражена в образе Герды. Таким образом, Герда и Снежная королева – две ипостаси возлюбленной, которые не соединяются в одной личности. Это холодные поцелуи бессердечной красавицы или сердечная дружба без намёка на эротические отношения.

4,4(24 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.04.2021

Освежающий и полезный напиток: лимонад из лаймов и имбиря...

Здоровье

23.09.2021

Как сохранить здоровые и крепкие зубы...

Финансы-и-бизнес

09.05.2023

Как эффективно организовать сбор средств для благотворительных целей?...

Компьютеры-и-электроника