Объяснение: 1) Задать формулой функцию, график которой проходит через точки А(1;1) и В(2;4). Решение : Уравнение прямой y=kx+b, Подставим в него вместо х и у координаты точек А и В, получим 2 уравнения: 1= k+b b и 4= 2k+b. Из первого уравнения b=1 - k, подставим во второе, получим 4= 2k+1-k ⇒k=3, b= 1-3=-2. Значит уравнение прямой у = 3х - 2.
2) Задать формулой функцию, график которой проходит через точки А(-12;-7) и В(15;2). Решение:равнение прямой y=kx+b, Подставим в него вместо х и у координаты точек А и В, получим 2 уравнения: -7 = -12k+b и 2 = 15k+b. Из второго уравнения b= 2-15k подставим в первое: -7 = -12k+2-15k ⇒ -9 = -27k ⇒k= 9/27=1/3 , тогда b= 2-15·1/3=2-5=-3. Уравнение прямой у= 1/3·х -3
№Задать формулой функцию, график которой проходит через точки А(-5;0) и В(12;-1). Решение аналогично: 0= -5k+b и -1 = 12k+b ⇒ k=1/17, b=5/17. Уравнение прямой у= 1/17·х +5/17
4)Задать формулой функцию, график которой проходит через точки А(0;3) и В(2;-1). Решение аналогично: 3= 0·k+b и -1= 2k+b ⇒b=3, k=(-1-b)/2=(-1-3)/2=-2 Уравнение прямой : у=-2х+3
Изначальное неравенство:
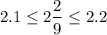
Оно нестрогое, так как скобки квадратные (данный промежуток является отрезком).
Чтобы не мучаться с неправильными дробями, вычтем из всего неравенства двойку. Так делать можно.
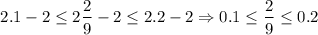
Запишем все в виде обыкновенных дробей
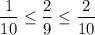
Тут вообще сразу видно, что правая часть неравенства не выполняется (это как при делении пирога: если делить его на большее количество, то каждому меньше достанется)
Чтобы не было недоразумений, докажу это:
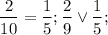
v - некоторый знак неравенства
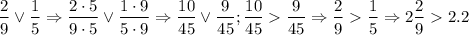
То есть наше число больше правой (большей) границы, а значит, оно НЕ принадлежит отрезку и записывается это таким образом:
![$\boxed{2\frac{2}{9}\notin [2.1; 2.2] }](/tpl/images/0305/3392/a9367.png)
y(1/3y+1)=0
y=0 или 1/3y+1=0
y+3=0
y=-3
ответ: -3,0