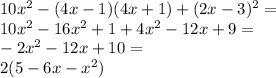
1) 3ˣ < 1 + 12·3⁻ˣ|·3ˣ; (3ˣ)² < 3ˣ + 12; (3ˣ)² - 3ˣ - 12 < 0; (3ˣ)² - 3ˣ - 12 = 0; - квадратное уравнение относительно 3ˣ, отсюда 3ˣ = 4 или 3ˣ = -3 - не имеет решений.
Рисунок во вложении
ответ: (-∞; log₃4)
2) 4·4ˣ < 7·2ˣ + 2; 4·4ˣ - 7·2ˣ - 2 < 0; 4·(2ˣ)² - 7·2ˣ - 2 = 0 - квадратное уравнение относительно 2ˣ, отсюда D = 49 + 32 = 81; √D = 9; 2ˣ = (7 + 9)/8 = 2 или 2ˣ = (7 - 9)/8 = -1/4 - не имеет решений.
Рисунок во вложении
ответ: (-∞; 1).
3) 9ˣ - 6·3ˣ - 27 = 0; (3ˣ)² - 6·3ˣ - 27 = 0; - квадратное уравнение относительно 3ˣ отсюда 3ˣ = 9; x = 2 или 3ˣ = -3 - не имеет решений.
ответ: 2.
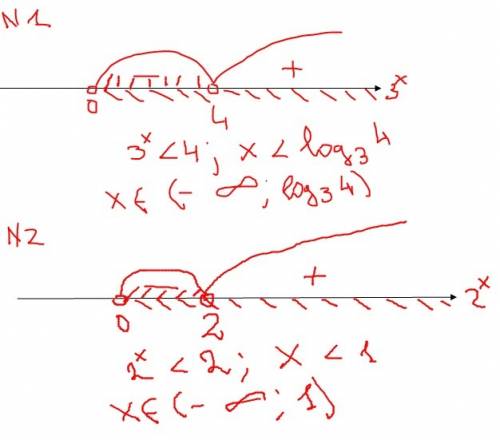
дано: авсд - параллелограмм
ам=мб мс=мд.
доказать: авсд - прямоугольник
доказательство: так как ам=мб ад=вс и мс=мд, то треугольники амд и амс равны по третьему признаку(по трём сторонам)
так как эти треугольники равны, то и углы у них равны(угол всм = углу мда; угол свм = углу дамЖ угол смв = углу дма) , нас интересуют углы дам и свм. они односторонние, значит их сумма должна быть 180 градусов (так как вс и ад параллельны а ав их пересекает, а при пересечении двух параллельных прямых третьей сумма односторонних углов равна 180 градусов). следовательно угол дам и угол сбм = 90 градусов, а если в параллелограмме хотябы один угол прямой, то это прямоугольник.