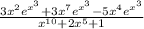
Объяснение:
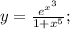
Производная дроби находится по следующей формуле:
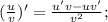
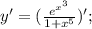
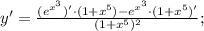
Функция
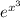
является сложной функцией. Производная сложной функции находится по следующей формуле:
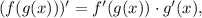
отсюда получаем
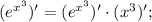
Если ввести замену
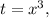
то выражение
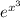
преобразуется как
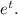
Производная последнего выражения является табличным значением:
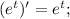
Возвращаясь к замене, получаем:
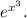
Производная второго множителя находится по следующей формуле:
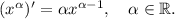
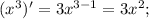
Подставим полученные значения в произведение:
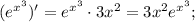
Подставим значение этой производной в дробь:
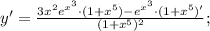
Производная суммы равна сумме производных:
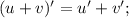
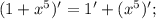
1 — константа. Производная константы равна нулю.
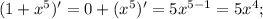
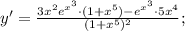
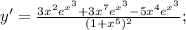
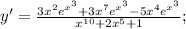
-х-2у= 8
-4х-у= - 3
умножаем первое уравнение на четыре, затем вычетаем из первого уравнения второе (обратите внимание на знаки!), получаем:
-7у = 35
у= - 5