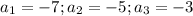

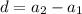
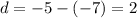
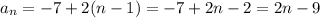
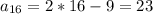
В первом подставим вместо x 5 получим [0/на чисто]а это есть 0
1)=0
2)подставим корень(3) получим (1+3-1)/3*3=3/9 или 1/3
3)подставим безконечность,получим [безконечность/бесконечность](а значит делим на большую степень т.е х^2)получим: (2+1/x +1/x^2)/(3+1/x^2) (опять подставим безконечность,и получим (число делённое на безконечность есть 0)а значит выходит) =2/3
4)подставим 0 получим [0/0] а значит надо умножить на сопряжонное и получим:
(x(sqrt(3)+x + sqrt(3)-x))/((sqrt(3)+x-sqrt(3)-x)(sqrt(3)+x-sqrt(3)-x)) (SQRT-корень квадратный) далее в знаменателе сокрощаем и получается там (sqrt(3)=x)^2-(sqrt(3)-x)^2
после упрощения и подстановки 0 получаем число/0 а это есть безконечность ответ:безконечность описаный выше с подстановкой безконечности,далее деим всё на x^4 и результат будет =5
5)поделим почленно 1/x^2-sqrt(1)/x^2 +x^2/x^2 ,далее сокращаем и останется x^2/x^2 а это 1 ответ 1
а) A= (x^12-1)/(x^4-1)=(x^4-1)(x^8+x^4+1)/(x^4-1)=x^8+x^4+1,
б) A= (x^12-1)/(x^2-1)=(x^2-1)(x^2+1)(x^8+x^4+1)/(x^2-1)=(x^2+1)(x^8+x^4+1),
в) A= (x^12-1)/(x^12-2)=1+1/(x^12-2)
г) A= (x^12-1)/(x+1)=(x+1)(x-1)(x^2+1)(x^8+x^4+1)/(x+1)=(x-1)(x^2+1)(x^8+x^4+1)
д) A=(x^12-1)/(x-1)=(x+1)(x-1)(x^2+1)(x^8+x^4+1)/(x-1)=(x+1)(x^2+1)(x^8+x^4+1)
е) A=(x^5-32)/(x-2)=(x-2)(x^4+2x^3+4x^2+8x+16)/(x-2)=(x^4+2x^3+4x^2+8x+16)
ж) A=(x^6-64)/(x-2)=(x-2)(x^5+2x^4+4x^3+8x^2+16x+32)/(x-2)= (x^5+2x^4+4x^3+8x^2+16x+32)
з) A=(x^7-128)/(x-2)=(x-2)(x^6+2x^5+4x^4+8x^3+16x^2+32x+64)/(x-2)= (x^6+2x^5+4x^4+8x^3+16x^2+32x+64)