y₁ = x² - 4x + 3; y₂ = x - 1
исследуем функцию y₁ = x² - 4x + 3
Нули функции:
x² - 4x + 3 = 0
D = 16 - 12 = 4
√D = 2
x₁ = (4 - 2):2 = 1
x₂ = (4 + 2):2 = 3
Вершина параболы: х = 4/2 = 2
у(2) = 4 - 4·2 + 3 = -1
Для определения пределов интегрирования найдёи точки пересечения функций
y₁ = x² - 4x + 3 и y₂ = x - 1
x² - 4x + 3 = х - 1
x² - 5x + 4 = 0
D = 25 - 16 = 9
√D = 3
x₁ = (5 - 3):2 = 1
x₂ = (5 + 3):2 = 4
Итак, нижний предел интегрирования x₁ = 1, верхний - x₂ = 4
Поскольку на интервале х∈(1,4) у₂ > у₁, то будем находить интеграл от разности
у₂ - у₁ = x - 1 - (x² - 4x + 3) = x - 1- x² + 4x - 3 = - x² + 5x - 4
∫(- x² + 5x - 4)dx = -x³/3 + 5x²/2 - 4x
Подставим пределы интегрирования
S = (-64/3 + 5·16/2 - 4·4) - (-1/3 + 5/2 - 4) = -64/3 + 40 - 16 +1/3 - 5/2 + 4 =
= - 21 + 28 - 2,5 = 4,5
Без взятия производных для определения наибольшего и наименьшего значений функции приходится строить график этой функции.
График функции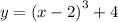 
можно получить из графика 
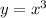следующим образом:
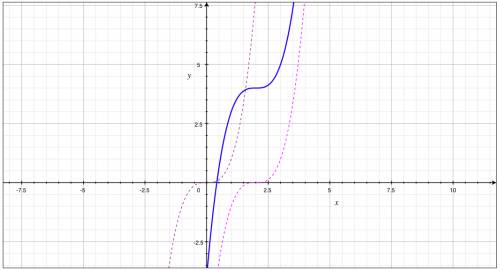
1. График 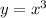сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
2. Полученный график y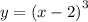
сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
Полученный график функции 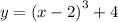показан самым жирным и самым синим на рисунке.
Из графика видим, что на отрезке ![\left[0;3\right]](/tpl/images/0129/5065/c1b3c.png)
рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
Итак, ответ.
![min|_{\left[0;3\right]} y(x) = y(0) = \left(0 - 2\right)^3 + 4 = -8 + 4 = -4](/tpl/images/0129/5065/af09b.png)
![max|_{\left[0;3\right]} y(x) = y(3) = \left(3 - 2\right)^3 + 4 = 1 + 4 = 5](/tpl/images/0129/5065/8238e.png)
(a^3+3a^2)+(9a-27) разделить на (a+3)=a^2(a+3)-9(a+3) деленое на (a+3)=(a+3)(a^2-9) делить на (a+3)=сокращаем (a+3) и остаеться a^2-9