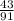
Объяснение:
Всего шаров 6+8 = 14
Вероятность того, что первый шар будет черным:
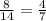
После того, как вынули черный шар, в ящике осталось 13 шаров, из которых 7 черных.Теперь вероятность того, что вытянутый шар будет черным:
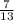
Вероятность того, что оба вынутых шара будут черными:
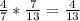
Теперь вычислим вероятность вынуть два белых шара.
Вероятность вынуть белый шар:
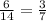
Вероятность вынуть второй белый шар:
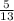
Вероятность того, что оба вынутых шара будут белыми:
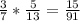
Теперь наконец-то вычислим вероятность того, что вынут два шара одного цвета (т.е. вынут два черных шара или два белых шара), используя правило сложения:
 .
.
![\left[\begin{array}{ccc}0&1&0\\0&0&1\\0&0&0\end{array}\right]](/tpl/images/0459/8733/0ef41.png)
![\left[\begin{array}{ccc}0&0&0\\1&0&0\\0&1&0\end{array}\right]](/tpl/images/0459/8733/bed8c.png)
![\left[\begin{array}{ccc}0&0&1\\0&0&0\\0&0&0\end{array}\right]](/tpl/images/0459/8733/dec6f.png)
![\left[\begin{array}{ccc}0&0&0\\0&0&0\\1&0&0\end{array}\right]](/tpl/images/0459/8733/14fe4.png)
![\left[\begin{array}{ccc}0&1&0\\0&0&1\\0&0&0\end{array}\right]](/tpl/images/0459/8733/0ef41.png) или
или![\left[\begin{array}{ccc}0&0&0\\1&0&0\\0&1&0\end{array}\right]](/tpl/images/0459/8733/f3b18.png)
0,0(1) = 0,0111111111...
Можно представить в виде бесконечной геометрической прогрессии
0,01 + 0,001 + 0,0001 ... ∞
Формула суммы бесконечно убывающей геометрической прогрессии :
2,3(1) = 2,3 + 1/90