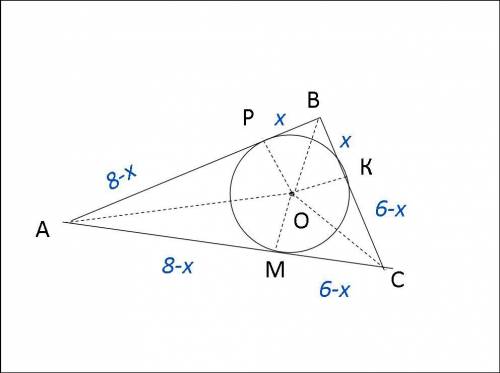
Пусть РВ=х
1. Рассмотрим Δ ОРВ и ΔОВК, у них
1) ОР=ОК=r , как радиусы одной окружности
2) Радиус, проведенный в точку касания всегда перпендикулярен касательной, поэтому
∠OPA=∠OКB=90°
3) ОВ - общая
Значит, Δ ОРВ = ΔОВК.
Отсюда РВ=ВК=х
2. Аналогично Δ КОС = ΔОМС, у них
1) ОМ=ОК=r , как радиусы одной окружности
2) Радиус, проведенный в точку касания всегда перпендикулярен касательной, поэтому
∠OКС=∠OМС=90°
3) ОС - общая
Значит, КС=МС=(6-х)
3. Так же Δ ОРА и ΔОМА, у них
1) ОР=ОМ=r , как радиусы одной окружности
2) Радиус, проведенный в точку касания всегда перпендикулярен касательной, поэтому
∠OPA=∠OМА=90°
3) ОА - общая
Значит, АР=АМ=(8-х)
4. Очевидно, что АС=АМ+МС
Подставим АС=12см
АМ=8-х
МС=6-м
Получаем уравнение:
12=(8-х)+(6-х)
2х=14-12
2х=2
х=2:2
х=1
РВ=ВК= 1 см, тогда
КС=МС=6-1=5см
АР=АМ=8-1=7см
в) Преобразуем числитель. (1-cos²x+sin²x)/(x*tg3x)=2sin²x/(x*tg3x), подведем данную запись под первый замечательный предел. При икс, стремящемся к нулю, sinx ; tg3x эквивалентны х и 3х соответственно, а потому получим предел дроби 2*х*х/(х*3х) и он равен 2/3.
ответ 2/3
г) преобразуем (4-x)*(㏑(2-3х)-㏑(5-3х))=(4-x)*(㏑((2-3х)/(5-3х))=
(4-x)㏑((3х-2)/(3х-5))=(4-x)㏑((1+3/(3x-5))=㏑((1+3/(3x-5))^(4-x)
cвели решение ко второму замечательному пределу, возьмем сначала предел от (1+3/(3x-5))^(4-x), а затем логарифм от полученного предела.
представим (1+3/(3x-5))⁽⁴ ⁻ˣ⁾=(((1+(3/(3x-5)))⁽³ˣ ⁻⁵⁾/³))⁽³⁽⁽⁴⁻ˣ⁾/⁽³ ˣ⁻⁵)предел от этого выражения равен е⁻¹, а ㏑е⁻¹=-1*lnе=-1
ответ -1