1/n*(n+1) = 1/n - 1/(n+1) используем эту формулу
1/(x + 2019)(x + 2020) + 1/(x + 2020)(x + 2021) + 1/(x + 2021)(x + 2022) + 1/(x + 2022)(x + 2023) = 1/999999
1/(x + 2019) - 1/(x + 2020) + 1/(x + 2020) - 1/(x + 2021) + 1/(x + 2021) - 1/(x + 2022) + 1/(x + 2022) - 1/(x + 2023) = 1/999999
1/(x + 2019) - 1/(x + 2023) = 1/999999
(x + 2023 - x - 2019)*999999 = (x + 2019)(x + 2023)
4*999999 = x² + 4042x + 2019*2023
x² + 4042x + 2019*2023 - 4*999999 = 0
4*999999 = 4*1000000 - 4 = 3999996
2019*2023 = (2021 - 2)(2021 + 2) = 4084441 - 4 = 4084437
x² + 4042 x + 84441 = 0
D = b² - 4ac = 4042² - 4*84441 = 4*2021² - 4*84441) = 4*(4084441 - 84441) = 4*4000000 = 2²*2000² = 4000²
x12 = (-4042 +- 4000)/2 = -4021 и -21
ответ -21 и -4021
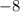
Объяснение:
Чтобы найти точку максимума, надо исследовать график производной на знак функции.
Найдём производную:
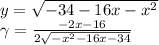
Чтобы найти точки максимума, приравняем производную к нулю.
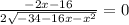
Дробь равняется нулю, если числитель дроби равняется нулю, а знаменатель существует:
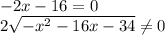
Решим их отдельно:
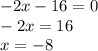
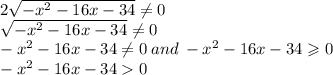
Решим нижнее неравенство методом интервалов. Для этого найдём корни уравнения
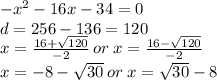
Метод интервалов подразумевает подстановку значений аргумента и установку знака функции.
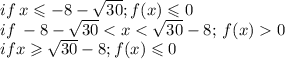
Нас удовлетворяет второе условие, значит
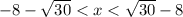
Проверим, входит ли корень числителя в ОДЗ знаменателя:
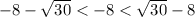
Корень входит в ОДЗ.
Исследуем график производной на знак функции:
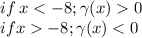
Знак функции сменяется с положительного на отрицательный, значит -8 - точка максимума.