

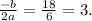 И ответ получаем точно такой же. Это объясняется тем, что, ища производную, мы нашли минимум функции (нулями производной может быть как минимум, так и максимум, надо смотреть на возрастание/убывание), который для параболы ветвями вверх и есть ее вершина. Таким образом, Вы можете смотреть по графику возрастание/убывание или искать с производной (это универсальнее).
И ответ получаем точно такой же. Это объясняется тем, что, ища производную, мы нашли минимум функции (нулями производной может быть как минимум, так и максимум, надо смотреть на возрастание/убывание), который для параболы ветвями вверх и есть ее вершина. Таким образом, Вы можете смотреть по графику возрастание/убывание или искать с производной (это универсальнее).