Получатся два прямоугольных треугольника, в каждом из которых данные отрезки d и m будут являться гипотенузами, их проекции d₁ и m₁ катетами, а расстояние между параллельными плоскостями h катет По условию d + m = 40 Пусть х - длина проекции d₁ (40 - m) - длина проекции m₁ Применяем теорему Пифагора для первого треугольника d² - d₁² = h² и для второго m² - m₁² = h² Правые части равны, приравняв левые части, получим уравнение 13² - x² = 37² - (40 - x)² 169 - x² = 1369 - 1600 + 80x - x² 80x = 400 x = 400 : 80 х = 5 см - длина первой проекции 40 - 5 = 35 см - длина второй проекции Ищем разность 35 - 5 = 30 см ответ: 30 см
Для условия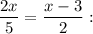
Умножим обе части уравнения на 10.
2x·2 = (x-3)·5
4x = 5x-15
+15 = 5x-4x
x = 15
ответ: x = 15.
Для условия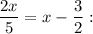
Умножим обе части уравнения на 10.
2x·2 = x·10-3·5
4x = 10x-15
+15 = 10x-4x
6x = 15
x =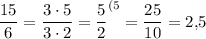
ответ: x = 2,5.