Дана функция f(x) = (-1/3)x³ (1/2)x² + 2х - 6.
Находим производную y'(x) = -x² - x + 2.
Определяем критические точки, приравняв производную нулю.
-x² - x + 2 = 0 или x² + x - 2 = 0.
Ищем дискриминант:
D=1^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√9-1)/(2*1)=(3-1)/2=2/2=1;
x_2=(-√9-1)/(2*1)=(-3-1)/2=-4/2=-2.
Получили 3 промежутка монотонности функции:
(-∞; -2), (-2; 1) и (1; +∞).
Находим знаки производной y' = -x² - x + 2 на этих промежутках
х = -3 -2 0 1 2
y' = -4 0 2 0 -4.
Там, где производная отрицательна - там функция убывает.
Это промежутки (-∞; -2) и (1; +∞).
14 часов занял весь путь, включая время на остановку
Объяснение:
Пройдённый путь S зависит от скорости υ и времени t по формуле
S = υ · t или t = S / υ.
Пусть половину пути автомашина проехала со скоростью υ км/час. Тогда время t₀, потраченное на половину пути, равна
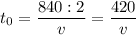часов или 
.
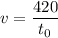По условию, на оставшийся путь автомашина потратила на час меньше за счет увеличения скорости на 10 км/час, то есть проехала (t₀-1) час со скоростью (υ +10) км/час. Поэтому
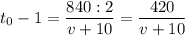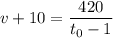или 
или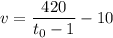 
.
Приравнивая скорость, получим:
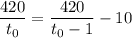
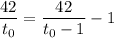
42·(t₀-1)=42·t₀-t₀·(t₀-1)
t₀²-t₀-42=0
D=(-1)²-4·1·(-42)=1+168=169=13²
t₀=(1-13)/2=-6 - не подходит, так как время не отрицательно.
t₀=(1+13)/2=7 часов на половину пути. Тогда на весь путь
2·7=14 часов.
