Вычисляем площадь прямоугольника на правом графике (K) площадь прямоугольника равна первой стороне помноженной на вторую
Вычисляем площадь фигуры на первом графике (Это площадь под графиком до графика f2(x)=2
Берём определённый интеграл где за нижний индекс будет выступать меньший корень уравнения находим корень меньший он равен -2 пишем в интеграл на нижний индекс -2 Это начало интегрирования (интеграл от до где начало а конец
мы нашли это -2 (нижний индекс)
это меньший корень уравнения он равен
определили точки интегрирования теперь ставим функцию которую интегрируем f(x) интегрируем по x
Площадь ограниченная графиком = равна площади прямоугольника без площади которую нам даст интеграл .
S=K-T
Описать как брать интеграл вручную не стану есть много литературы в нете и это долго .
Можно попробовать разбить на систему неравенств: 1/3≤(x^2-x+1)/(x^2+x+1) и (x^2-x+1)/(x^2+x+1)≥3 после приведения к общему знаменателю, переносу в левую часть и упрощения получаем: (x-1)^2/(3(x^2+x+1))≥0 и -(x+1)^2/(x^2+x+1)≤0 далее рассуждаем: первое неравенство- дробь больше или равна нулю в двух случаях, когда числитель больше или равен нулю, знаменатель больше нуля и когда числитель меньше или равен нулю и знаменатель меньше нуля. В нашем случае, независимо от значений x, числитель больше или равен нулю, знаменатель всегда строго больше нуля. Следовательно данная дробь всегда положительна. Аналогичные рассуждения со второй дробью. Она всегда отрицательна или равна нулю- числитель при любых x отрицательный, а при x=-1 равен нулю. А знаменатель всегда положительный. Следовательно выполняется указанное двойное неравенство. ч.т.д.
Можно попробовать разбить на систему неравенств: 1/3≤(x^2-x+1)/(x^2+x+1) и (x^2-x+1)/(x^2+x+1)≥3 после приведения к общему знаменателю, переносу в левую часть и упрощения получаем: (x-1)^2/(3(x^2+x+1))≥0 и -(x+1)^2/(x^2+x+1)≤0 далее рассуждаем: первое неравенство- дробь больше или равна нулю в двух случаях, когда числитель больше или равен нулю, знаменатель больше нуля и когда числитель меньше или равен нулю и знаменатель меньше нуля. В нашем случае, независимо от значений x, числитель больше или равен нулю, знаменатель всегда строго больше нуля. Следовательно данная дробь всегда положительна. Аналогичные рассуждения со второй дробью. Она всегда отрицательна или равна нулю- числитель при любых x отрицательный, а при x=-1 равен нулю. А знаменатель всегда положительный. Следовательно выполняется указанное двойное неравенство. ч.т.д.
Вычисляем площадь прямоугольника на правом графике (K) площадь прямоугольника равна первой стороне помноженной на вторую
Вычисляем площадь фигуры на первом графике (Это площадь под графиком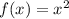 до графика f2(x)=2
до графика f2(x)=2
Берём определённый интеграл где за нижний индекс будет выступать меньший корень уравнения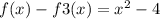 находим корень меньший он равен -2 пишем в интеграл на нижний индекс -2 Это начало интегрирования (интеграл от
находим корень меньший он равен -2 пишем в интеграл на нижний индекс -2 Это начало интегрирования (интеграл от 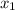 до
до 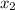 где начало
где начало 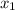 а конец
а конец 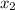
определили точки интегрирования теперь ставим функцию которую интегрируем f(x) интегрируем по x
Площадь ограниченная графиком = равна площади прямоугольника без площади которую нам даст интеграл .
S=K-T
Описать как брать интеграл вручную не стану есть много литературы в нете и это долго .