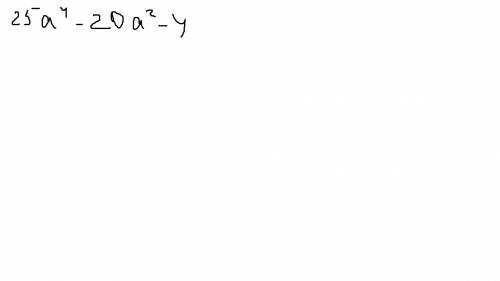
Объяснение:
Последовательность называется возрастающей, если для любого n∈N выполняется неравенство yn<yn+1.
Последовательность называется убывающей, если для любого n∈N выполняется неравенство yn>yn+1.
Выпишем n-й и n+1-й члены последовательности: yn=n213n, yn+1=(n+1)213n+1.
Чтобы сравнить эти члены, составим их разность и оценим её знак:
yn+1−yn=(n+1)213n+1−n213n=(n2+2n+1)−13n213n+1=2n+1−12n213n+1
Для натуральных значений n справедливы неравенства 2n≤6n2 и 1<6n2.
Сложив их, получим 1+2n<12n2, т.е. для любых натуральных значений n справедливо неравенство 2n+1−12n213n+1<0, значит, yn+1−yn<0.
Итак, для любых натуральных значений n выполняется неравенство yn+1<yn,
а это значит, что последовательность (yn) убывает.
правильного двенадцатиуголника
количество сторон тоже 12
каждая сторона - это основание равнобедренного треугольника с вершиной в центре
правильного двенадцатиуголника
величина угла при вершине 360/12=30
углы при основании (180-30) /2 =75
пусть боковая сторона каждого треугольника -b
тогда по теореме косинусов
a^2 = b^2 +b^2 -2*bb*cos30
a^2 = 2b^2(1-cos30) =2b^2(1-√3/2)=b^2(2-√3)
b^2 =a^2 / (2-√3)
площадь одного треугольника
S1 =1/2*b^2*sin30 =b^2/4 <---подставим b^2
S1 =a^2 / 4(2-√3) <---домножим числ. и знамен. на (2+√3)
S1 =a^2(2+√3) / 4(2-√3)(2+√3) =a^2(2+√3) / 4(4-3) =a^2(2+√3) / 4
общая площадь S= 12*S1 =12*a^2(2+√3) / 4 = 3a² (2+√3).
ДОКАЗАНО