Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру
r=S:p, где р - полупериметр
Треугольник тоже многоугольник, и радиус вписанной в него окружности найдем по этой формуле.
Чтобы найти площадь треугольника, нужно знать его третью сторону, основание.
Высота известна, боковая сторона - тоже.
Высота делит равнобедренный треугольник на два равных прямоугольных, в которых боковая сторона - гипотенуза. высота и половина основания - катеты..
Найдем половину основания по т.Пифагора:
0,5а=√(225-144)=9 см
Основание равно 2*9=18 см
Площадь треугольника
S=ah:2=18*12:2=108 см²
полупериметр
р=(18+30):2=24
r=108:24=4,5 см
Треугольник равнобедренный. Для вписанной в равнобедренный треугольник окружности, когда известны все стороны и высота, можно вывести формулу:
r=0,5*bh:0,5(2a+b)
или произведение высоты на основание, деленное на периметр.
r=bh:Р
r=18*12:(30+18)=4,5
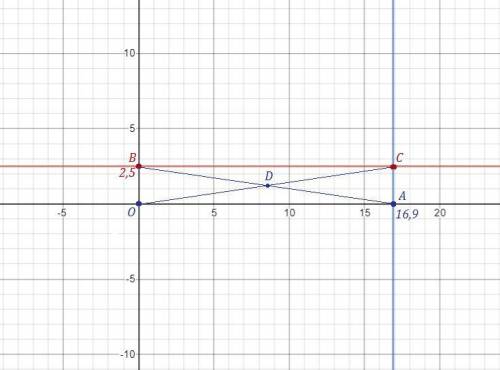
1) Четырёхугольник ABCD является параллелограммом, если его противоположные стороны попарно равны, то есть AB=CD , BC=AD.
Если у параллелограмма равны диагонали, то этот параллелограмм является прямоугольником, то есть АС=BD .
Проверим это.
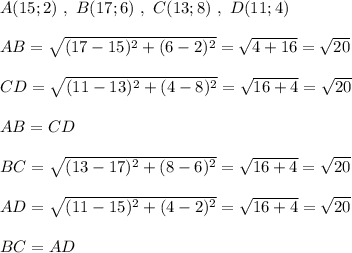
Так как мы получили, что не только противоположные стороны попарно равны , но равны все стороны четырёхугольника , то этот четырёхугольник - параллелограмм, являющийся либо ромбом, либо квадратом.
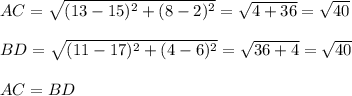
Равны диагонали . Значит АВСD - прямоугольник .
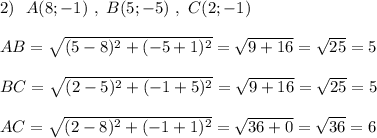
Так как две стороны треугольника равны, то треугольник равнобедренный .
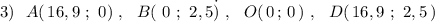
Координаты точки пересечения диагоналей можно найти как координаты середины отрезка АВ ( или ОС ), так как диагонали прямоугольника в точке пересечения делятся пополам .
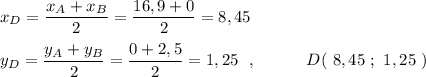
X1 = (26 +30) /14 = 4
X2 = (26 -30) /14 = -4/14