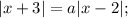 Конечно, решаем графически. Строим график
Конечно, решаем графически. Строим график 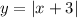 , я думаю, тут легко - смещение на 3 ед. влево по OX, график - "галка". Второй график зависит от параметра и тут рассматриваем
, я думаю, тут легко - смещение на 3 ед. влево по OX, график - "галка". Второй график зависит от параметра и тут рассматриваем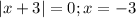 , корень один, подойдёт.
, корень один, подойдёт.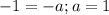 . В итоге получаем, что a=0, a=1. Иначе (a>1) будут 2 точки пересечения
. В итоге получаем, что a=0, a=1. Иначе (a>1) будут 2 точки пересечения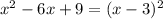 , строим обычную параболу
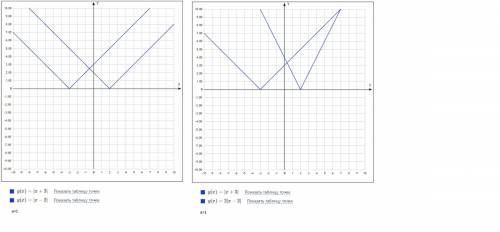
, строим обычную параболу 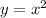 , только сместим её на 3 ед. вправо по OX.
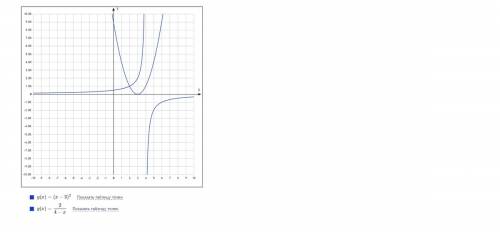
, только сместим её на 3 ед. вправо по OX.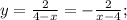 можно построить
можно построить 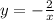 , посчитать несколько значений, потом сместить график на 4 ед. вправо по OX (он до переноса располагался во 2 и 4 четвертях, так как есть знак "-"). Есть красивый корень x=-2
, посчитать несколько значений, потом сместить график на 4 ед. вправо по OX (он до переноса располагался во 2 и 4 четвертях, так как есть знак "-"). Есть красивый корень x=-2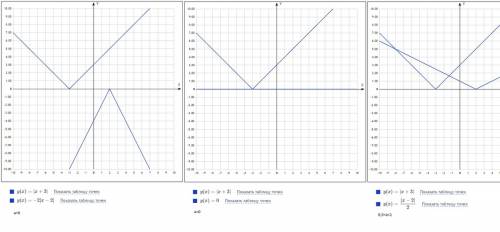
(sin2x*cos3x)/(cos2x) +sin3x-√2sin5x=0
(sin2x*cos3x+sin3x*cos2x)/(cos2x)-√2sin5x=0
sin(3x+2x)/(cos2x)-√2sin5x=0
(sin5x)/(cos2x)-√2sin5x=0
-sin5x-√2sin5x*cos2x=0
-sin5x(1+√2cos2x)=0
sin5x=0
5x=πk
x=πk/5
cos2x=-1/√2
2x=±3π/4+2πn
x=±3π/8+πn