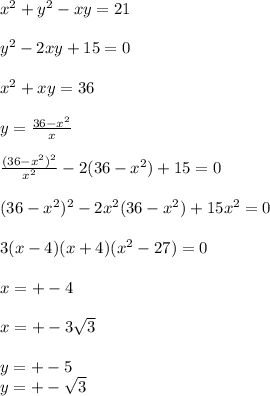
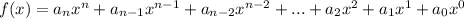 ,
, 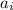 - коэффициент
- коэффициент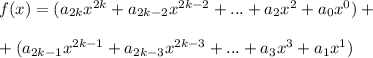
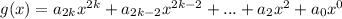
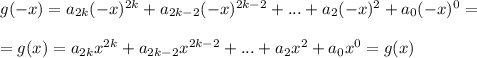
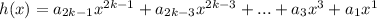

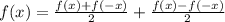


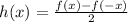

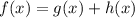 , где g(x) - чётная, а h(x) - нечётная функция.
, где g(x) - чётная, а h(x) - нечётная функция.b=+-2
Объяснение:
Пусть x1=a-один из корней уравнения, тогда второй корень x2=0,4 *a (40% от первого)
Тогда ,по теореме Виета :сумма корней равна второму члену взятому с противоположным знаком .
x1+x2=a+0,4*a =4,2b^2 -1,4
1,4*a=4,2b^2-1,4 (делим на 1,4 обе части уравнения)
1) a=3b^2-1 →a^2=(3b^2-1)^2= 9b^4-6b^2+1
Так же, по теореме Виета: произведение корней равно последнему члену.
x1*x2=a*0,4a=11,6b^2+2
0,4*a^2=11,6*b^2+2 (делим на 0,4 обе части уравнения)
2)a^2=29b^2+5
Подставляя 1 в 2 имеем:
9b^4-6b^2+1=29b^2+5
9b^4-35b^2-4=0 (биквадратное уравнение)
b^2=t>=0
9t^2 -35t-4=0
D=(-35)^2 - 4*9*(-4) =1225 +144=1369
√D=√1369=37
t=(35+-37)/18
t1=(35+37)/18=72/18=4
t2=(35-37)/18 <0 (не подходит)
b^2=4
b=+-2
Cделаем проверку: (b^2=4)
x^2 -(4,2*4-1,4)*x +11.6*4 +2=0
x^2-15,4*x +48,4=0
По теореме Виета:
a+0,4a=15,4
1,4a=15,4
a=15,4/1,4=11
x1=11 x2=0,4*11=4,4
x1*x2=11*4,4=48,4 (верно)
ответ: b=+-2