Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть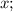 
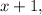
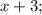
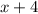- пять последовательных натуральных чисел, тогда их сумма равна:
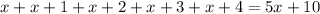
Очевидно, что каждое слагаемое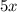 
и 
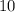делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть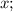 
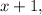
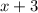- четыре последовательных натуральных числа, тогда их сумма равна:
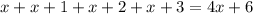
Очевидно, что первое слагаемое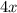 
делится на 4, а второе слагаемое 
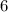не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть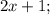 
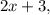
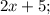
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
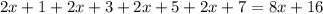
Очевидно, что каждое слагаемое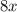 
и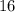 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть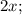 
; 
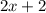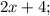
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
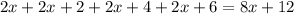
Очевидно, что каждое слагаемое 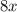и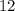 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.
В решении.
Объяснение:
Решите задачу с составления уравнения. Разность двух чисел равна 3, а разность их квадратов 69. Найдите эти числа.
х - первое число.
у - второе число.
По условию задачи система уравнений:
х - у = 3
х² - у² = 69
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 3 + у
(3 + у)² - у² = 69
9 + 6у + у² - у² = 69
6у = 69 - 9
6у = 60
у = 60/6
у = 10 - второе число.
х = 3 + у
х = 3 + 10
х = 13 - первое число.
Проверка:
13 - 10 = 3, верно.
13² - 10² = 169 - 100 = 69, верно.
