1) Используя формулу n-го члена арифметической прогрессии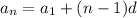 
, вычислим двадцатый член этой прогрессии:
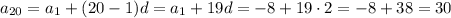
ответ: 30.
2) Формула суммы первых n членов арифметической прогрессии следующая: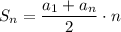 
Найдем же сначала восемнадцатый член арифметической прогрессии
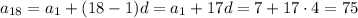
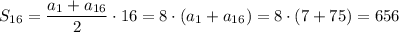
ответ: 656.
3) Первый член: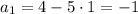 
Второй член: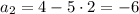 
Третий член: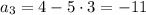 
Как видно, каждый последующий член уменьшается на (-5),т.е. это разность d = -5, следовательно, последовательность является арифметической прогрессией.
4) Используя n-ый член арифметической прогрессии, найдем ее разность
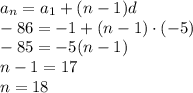
Да, является арифметической прогрессией.
5) Данная последовательность является арифметической прогрессии с первым членом 
и разностью прогрессии d=1
Всего таких членов не трудно посчитать по формуле n-го члена арифметической прогрессии:
То есть, нужно посчитать сумму первых 91 членов арифметической прогрессии
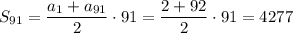
ответ: 4277.
Первое, что делаешь, находишь производную функции. производная = 2 cosх-4sin2х.
Дальше находишь критические точки, т.е. те точки, в которых производная равна нулю, а потом проверяешь, входят ли данные точки в промежуток.
2 cosx-4sin2x=0
2cosx-8sinx *4cosx=0/2
cosх-4sinx*2сosx=0
2cosx*4sinx-cosx=0
2cosx(4sinx-1/2)=0
2cos x=0 или 4 sinx-1/2=0
cosx=0 4 sinx=1/2, sinx=1/4, решаешь это уравнение и проверяешь, входит ли корень этого уравнения в указанный в задании промежуток!
x=pi/2+pik, k принадлежит z - так, как и первый корень проверяешь, принадлежит ли данному отрезку.
Потом вычисляешь значение функции на концах отрезках, т.е. 0 и 3pi/2 подставляешь, вместо х в саму функцию, и считаешь.
a) 6x - 12 = 4x - 8,
6х - 4х = -8 + 12,
2х = 4,
х = 4 : 2,
х = 2;
б) 2/3x = 18,
х = 18 : (2/3),
х = 18 · 3/2,
х = 27;
в) (2x - 5) - (3x - 7) = 4,
2х - 5 - 3х + 7 = 4,
-х + 2 = 4,
-х = 4 - 2,
-х = 2,
х = -2;
г) 5(x - 1,2) - 3x = 2,
5х - 6 - 3х = 2,
2х - 6 = 2,
2х = 2 + 6,
2х = 8,
х = 8 : 2,
х = 4.